题目内容
18.命题“?x0∈R,x0+1<0或${x_0}^2-{x_0}>0$”的否定形式是( )| A. | ?x0∈R,x0+1≥0或${x_0}^2-{x_0}≤0$ | B. | ?x0∈R,x0+1≥0或${x_0}^2-{x_0}≤0$ | ||
| C. | ?x0∈R,x0+1≥0且${x_0}^2-{x_0}≤0$ | D. | ?x0∈R,x0+1≥0且${x_0}^2-{x_0}≤0$ |
分析 根据命题否定的定义判断即可.
解答 解:命题“?x0∈R,x0+1<0或${x_0}^2-{x_0}>0$”的否定形式是:
?x0∈R,x0+1≥0且${{x}_{0}}^{2}$-x0≤0,
故选:D.
点评 本题考察了命题的否定,是一道基础题.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
9.已知直线y=kx-1与直线x+2y+3=0垂直,则k的是( )
| A. | 3 | B. | 1 | C. | -1 | D. | 2 |
6.过抛物线y=x2的焦点F作直线交抛物线于P,Q,若线段PF与QF的长度分别为m,n,则2m+n的最小值为( )
| A. | $\frac{3}{2}$ | B. | $\sqrt{2}$ | C. | $\frac{{3+2\sqrt{2}}}{4}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
13.已知扇形的中心角为$\frac{π}{3}$,半径为2,则其面积为( )
| A. | $\frac{π}{6}$ | B. | $\frac{4π}{3}$ | C. | $\frac{π}{3}$ | D. | $\frac{2π}{3}$ |
8.已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别为F1,F2,点M在双曲线上,且$\frac{|M{F}_{1}|}{|M{F}_{2}|}$=$\frac{\sqrt{5}-1}{\sqrt{5}+3}$.则双曲线C离心率的最大值为( )
| A. | $\sqrt{5}$+2 | B. | $\frac{\sqrt{5}+2}{2}$ | C. | $\sqrt{5}$-1 | D. | $\frac{\sqrt{5}+1}{2}$ |
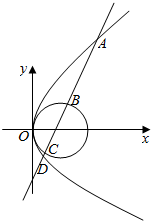 如图,直线y=$\frac{\sqrt{3}}{3}$(x-2)与圆(x-2)2+y2=4及抛物线y2=8x依次交于A,B,C,D四点,则|AB|+|CD|=28.
如图,直线y=$\frac{\sqrt{3}}{3}$(x-2)与圆(x-2)2+y2=4及抛物线y2=8x依次交于A,B,C,D四点,则|AB|+|CD|=28.