题目内容
8.设f(x)=mx2+(m+4)x+3.(1)试确定m的值,使得f(x)有两个零点,且f(x)的两个零点的差的绝对值最小,并求出这个最小值;
(2)若m=-1时,在[0,λ](λ为正常数)上存在x使f(x)-a>0成立,求a的取值范围.
分析 (1)f(x)为二次函数,令△>0得出m的取值范围,根据根与系数得关系用m表示两根的绝对值,求出新函数的最小值即可.
(2)求出f(x)在[0,λ]上的最大值fmax(x),则a<fmax(x).
解答 解:(1)∵f(x)有两个零点,∴$\left\{\begin{array}{l}{m≠0}\\{(m+4)^{2}-12m>0}\end{array}\right.$,解得m≠0.
设f(x)的两个零点为x1,x2,则x1+x2=-$\frac{m+4}{m}$,x1x2=$\frac{3}{m}$.
∴|x1-x2|2=(x1+x2)2-4x1x2=($\frac{m+4}{m}$)2-$\frac{12}{m}$=$\frac{16}{{m}^{2}}$-$\frac{4}{m}$+1=16($\frac{1}{m}$-$\frac{1}{8}$)2+$\frac{3}{4}$.
∴当m=8时,∴|x1-x2|2取得最小值$\frac{3}{4}$.∴|x1-x2|的最小值为$\frac{\sqrt{3}}{2}$.
(2)当m=-1时,f(x)=-x2+3x+3,f(x)的对称轴为x=$\frac{3}{2}$.
①若0$<λ<\frac{3}{2}$,则fmax(x)=f(λ)=-λ2+3λ+3,
②若$λ≥\frac{3}{2}$,则fmax(x)=f($\frac{3}{2}$)=$\frac{21}{4}$.
∵在[0,λ](λ为正常数)上存在x使f(x)-a>0成立,∴a<fmax(x).
综上,当0$<λ<\frac{3}{2}$时,a的取值范围是(-∞,-λ2+3λ+3);
当$λ≥\frac{3}{2}$时,a的取值范围是(-∞,$\frac{21}{4}$).
点评 本题考查了二次函数的零点个数与系数的关系,二次函数的单调性与最值,属于中档题.

| A. | $4\sqrt{2}π$ | B. | $8\sqrt{2}π$ | C. | 4π | D. | $4\sqrt{2}π+4π$ |
| A. | $\frac{2-\sqrt{3}}{4}$ | B. | $\frac{\sqrt{2}-\sqrt{6}}{4}$ | C. | $\frac{2±\sqrt{3}}{4}$ | D. | $\frac{\sqrt{2}±\sqrt{6}}{4}$ |
| A. | 向左平移$\frac{5π}{12}$个单位 | B. | 向右平移$\frac{5π}{12}$个单位 | ||
| C. | 向左平移$\frac{π}{6}$个单位 | D. | 向右平移$\frac{π}{6}$个单位. |
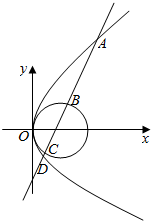 如图,直线y=$\frac{\sqrt{3}}{3}$(x-2)与圆(x-2)2+y2=4及抛物线y2=8x依次交于A,B,C,D四点,则|AB|+|CD|=28.
如图,直线y=$\frac{\sqrt{3}}{3}$(x-2)与圆(x-2)2+y2=4及抛物线y2=8x依次交于A,B,C,D四点,则|AB|+|CD|=28. 如图,在三棱锥K-ABC中,平面KAC⊥平面ABC,KC⊥AC,AC⊥AB,H为KA的中点,KC=AC=AB=2.
如图,在三棱锥K-ABC中,平面KAC⊥平面ABC,KC⊥AC,AC⊥AB,H为KA的中点,KC=AC=AB=2.