题目内容
直线3x-4y+k=0在两坐标轴上的截距之和为2，则实数k= ．
考点：直线的截距式方程
专题：直线与圆
分析：根据直线3x-4y+k=0的方程，分别令x，y分别为0，可得截距，进而可得答案．
解答：
解：因为直线的方程为：3x-4y+k=0，
令x=0，可得y=
，令y=0，可得x=-
，
故直线在两坐标轴上的截距之和为
-
=2，解得k=-24．
故答案为：-24．
令x=0，可得y=
| k |
| 4 |
| k |
| 3 |
故直线在两坐标轴上的截距之和为
| k |
| 4 |
| k |
| 3 |
故答案为：-24．
点评：本题考查直线的一般式方程与直线的截距式方程，涉及截距的求解，属基础题．
练习册系列答案
相关题目
函数f（x）=|x+2|的单调递减区间是（ ）
| A、（-∞，-2] |
| B、（-∞，2] |
| C、（-∞，0] |
| D、无减区间 |
递增等差数列{an}中，若a1+a9=0，则Sn取最小值时n等于（ ）
| A、4 | B、5 | C、6 | D、4或5 |
已知a，b是正实数，A是a，b的等差中项，G是a，b等比中项，则（ ）
| A、ab≤AG |
| B、ab≥AG |
| C、ab≤|AG| |
| D、ab＞AG |
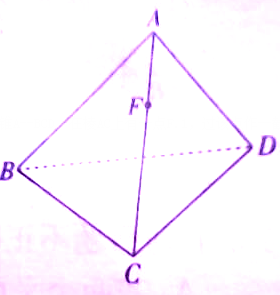如图三棱锥A-BCD，在棱AC上有一点F．