题目内容
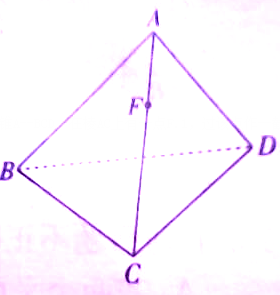如图三棱锥A-BCD，在棱AC上有一点F．（1）过该点作一截面与两棱AB，CD平行；
（2）求证：该截面为平行四边形．
考点：直线与平面平行的判定,平面的基本性质及推论
专题：空间位置关系与距离
分析：（1）根据线线平性的定理，即可做出截面．
（2）根据线线平行的性质定理和线面平行的性质定理，可得EH∥FG，EF∥GH，即而得到四边形EFGH是平行四边形
（2）根据线线平行的性质定理和线面平行的性质定理，可得EH∥FG，EF∥GH，即而得到四边形EFGH是平行四边形
解答：
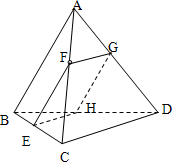解：（1）如图，过点F作直线FE∥AB，交BC于E，过点E作直线EH∥CD，交BD于H，过点F作直线FG∥CD，交AD于G，连接GH，
则四边形FEHG即为所求的截面，
（2）∵EH∥CD，FG∥CD
∴EH∥FG，
∴EH，FG确定一个平面，
∴EF?平面FEHG，
∵FE∥AB，平面FEHG∩平面ACD=GH，
∴EF∥GH
∴四边形EFGH是平行四边形
解：（1）如图，过点F作直线FE∥AB，交BC于E，过点E作直线EH∥CD，交BD于H，过点F作直线FG∥CD，交AD于G，连接GH，则四边形FEHG即为所求的截面，
（2）∵EH∥CD，FG∥CD
∴EH∥FG，
∴EH，FG确定一个平面，
∴EF?平面FEHG，
∵FE∥AB，平面FEHG∩平面ACD=GH，
∴EF∥GH
∴四边形EFGH是平行四边形
点评：本题考查的知识点是棱锥的结构特征，特殊四边形的判定，熟练掌握棱锥的结构特征是解答的关键．
练习册系列答案
阅读快车系列答案
相关题目
底面半径为1的圆锥侧面展开图是一个圆心角为直角的扇形，则该圆锥的体积为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若目标函数z=ax+by（a＞0，b＞0）满足约束条件
且最大值为40，则
+
的最小值为（ ）
|
| 5 |
| a |
| 1 |
| b |
A、
| ||
B、
| ||
| C、1 | ||
| D、4 |
设f（x）=
，h（x）=
，则f（h（e））等于（ ）
|
|
| A、1 | B、0 | C、-1 | D、e |
已知互相垂直的两条直线y=kx和y=-
分别与双曲线2x2-y2=1交于点A、B，点P在线段AB上，且满足
•
=
•
，则所有的点P在（ ）
| x |
| k |
| OA |
| OP |
| OB |
| OP |
| A、双曲线2x2-y2=1上 |
| B、圆x2+y2=1上 |
| C、椭圆上 |
| D、|x|+|y|=1上 |
“φ=
”是y=cos（x+φ）为奇函数的（ ）
| π |
| 2 |
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
