Question

已知某几何体的直观图和三视图如下如所示，其正视图为矩形，侧视图为等腰直角三角形，俯视图为直角梯形．

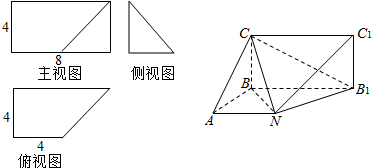
（Ⅰ）证明：BN⊥平面C₁B₁N；
（Ⅱ）设直线C₁N与平面CNB₁所成的角为θ，求cosθ的值．

Answer 1

考点：直线与平面所成的角,异面直线及其所成的角,直线与平面垂直的判定

专题：空间位置关系与距离,空间角

分析：（I）方法一先由题意判断出该几何体的直观图，利用直线与平面垂直的判定定理证明；方法二：利用空间向量的数量积，结合线面垂直的判定定理证明即可；
（II）方法一，先利用等体积法可求C₁到面CB₁N的距离，找出角，然后求解；方法二，利用空间向量法，求出直线的方向向量，平面的法向量然后求解即可．

解答： 解：（1）证明：方法一：由题意：该几何体的正视图其轮廓为矩形，侧视图为等腰直角三角形，俯视图为直角梯形．

则B₁C₁⊥面ABB₁N，且在面ABB₁N内，易证∠BNB₁为直角．
∵B₁C₁⊥面ABB₁N，且BN?面ABB₁N，
∴B₁C₁⊥BN
又∵BN⊥B₁N，且B₁N∩B₁C₁=B₁，
∴BN⊥面B₁NC₁
方法二：该几何体的正视图其轮廓为矩形，侧视图为等腰直角三角形，俯视图为直角梯形，则BA，BC，BB₁两两垂直．以BA，BC，BC₁分别为x，y，z轴建立空间直角坐标系，

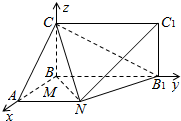
则N（4，4，0），B₁（0，8，0），C₁（0，8，4），C（0，0，4），
∵

BN

•

NB1

=0，

BN

•

B1C1

=0
∴BN⊥NB₁，且BN∩B₁C₁，
又∵B₁N∩B₁C₁=B₁∴BN⊥面B₁NC₁
（2）方法一：利用等体积法可求C₁到面CB₁N的距离为h=

4 6

3

，
则直线C₁N与平面CNB₁所成的角θ的正弦值为sinθ=

2

3

，从而cosθ=

7

3

方法二：设

n

=(x0，y0，z0)为平面CNB₁的一个法向量，
则

n • CN =0 n • NB1 =0

即

x0+y0-z0=0 x0-y0=0

，令x₀=1，则

n

=(1，1，2)．
又

C1N

=(4，-4，-4)．
则sinθ=|cos＜

n

，

C1N

＞|=

2

3

，从而cosθ=

7

3

点评：本题考查的知识点线面垂直的判定定理；线面角，考查空间想象能力以及计算能力．