题目内容
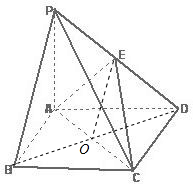
如图，已知四棱锥P-ABCD底面ABCD为矩形．PA=AD，侧面PAD垂直于底面ABCD，E是PD的中点．（Ⅰ）求证：PB∥平面AEC；
（Ⅱ）求证：平面PDC⊥平面AEC．
考点：平面与平面垂直的判定,直线与平面平行的判定
专题：空间位置关系与距离
分析：（1）连接BD交AC于O点，连接EO，只要证明EO∥PB，即可证明PB∥平面AEC；
（2）要证平面PDC⊥平面AEC，需要证明CD⊥AE，AE⊥PD，即垂直平面AEC内的两条相交直线．
（2）要证平面PDC⊥平面AEC，需要证明CD⊥AE，AE⊥PD，即垂直平面AEC内的两条相交直线．
解答：
解：（1）连接BD交AC于O点，连接EO，
∵O为BD中点，E为PD中点，
∴以EO∥PB，（2分）
又∵EO?平面AEC，PB?平面AEC，
∴PB∥平面AEC；（6分）
（2）∵侧面PAD垂直于底面ABCD，侧面PAD∩底面ABCD=AD，CD⊥AD，
∴CD⊥平面PAD．（8分）
∵AE?平面PAD，
∴CD⊥AE．（10分）
∵PA=AD，E为PD中点，
∴AE⊥PD．
∵CD∩PD=D，
∴AE⊥平面PDC．（12分）
又∵AE?平面PAD，
∴平面PDC⊥平面AEC．（14分）
∵O为BD中点，E为PD中点，
∴以EO∥PB，（2分）
又∵EO?平面AEC，PB?平面AEC，
∴PB∥平面AEC；（6分）
（2）∵侧面PAD垂直于底面ABCD，侧面PAD∩底面ABCD=AD，CD⊥AD，
∴CD⊥平面PAD．（8分）
∵AE?平面PAD，
∴CD⊥AE．（10分）
∵PA=AD，E为PD中点，
∴AE⊥PD．
∵CD∩PD=D，
∴AE⊥平面PDC．（12分）
又∵AE?平面PAD，
∴平面PDC⊥平面AEC．（14分）
点评：本题考查直线与平面平行，平面与平面垂直的判定，逻辑思维能力，是中档题．
练习册系列答案
相关题目
如图，在四棱锥P-ABCD中，PA⊥平面ABCD，四边形ABCD为平行四边形，AB=1，AC=1，BC=