题目内容
已知m,n是正整数,f(x)=(1+x)m+(1+x)n的展开式中x的系数为7,求f(x)展开式中x2的系数的最小值,并求这时f(0.003)的近似值(精确到0.01).
考点:二项式定理
专题:二项式定理
分析:由题意可得m+n=7≥2
,求得mn最大为12,f(x)展开式中x2的系数为
+
=
,由此求得f(x)展开式中x2的系数的最小值.再利用二项式定理求得f(0.03)的近似值.
| mn |
| C | 2 m |
| C | 2 n |
| (m+n)2-2mn-7 |
| 2 |
解答:
解:由题意可得m+n=7≥2
,∴mn≤
,故mn最大为12,此时,m、n一个为3,另一个为4.
∵f(x)展开式中x2的系数为
+
=
+
=
=
=
≥
=9,
即f(x)展开式中x2的系数的最小值为9.
f(0.03)=(1+0.03)4+(1+0.03)3≈(1+
×0.03)+(1+
×0.03)=2.21,
即f(0.003)的近似值为 2.21.
| mn |
| 49 |
| 4 |
∵f(x)展开式中x2的系数为
| C | 2 m |
| C | 2 n |
| m(m-1) |
| 2 |
| n(n-1) |
| 2 |
| m2+n2-(m+n) |
| 2 |
| m2+n2-7 |
| 2 |
=
| (m+n)2-2mn-7 |
| 2 |
| 49-24-7 |
| 2 |
即f(x)展开式中x2的系数的最小值为9.
f(0.03)=(1+0.03)4+(1+0.03)3≈(1+
| C | 1 4 |
| C | 1 3 |
即f(0.003)的近似值为 2.21.
点评:本题主要考查二项式定理的应用,二项式系数的性质,二项式展开式的通项公式,求展开式中某项的系数,近似计算,属于基础题.

练习册系列答案
相关题目
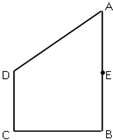 如图所示,在直角梯形ABCD中,E是AB的中点,∠B=∠C=90°,
如图所示,在直角梯形ABCD中,E是AB的中点,∠B=∠C=90°, 如图,已知四棱锥P-ABCD底面ABCD为矩形.PA=AD,侧面PAD垂直于底面ABCD,E是PD的中点.
如图,已知四棱锥P-ABCD底面ABCD为矩形.PA=AD,侧面PAD垂直于底面ABCD,E是PD的中点.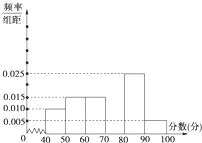 某中学团委组织了“弘扬奥运精神,爱我中华”的知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后画出如图所示部分频率分布直方图.观察图形给出的信息,回答下列问题:
某中学团委组织了“弘扬奥运精神,爱我中华”的知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后画出如图所示部分频率分布直方图.观察图形给出的信息,回答下列问题: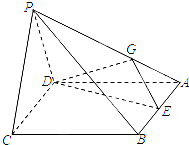 如图,四棱锥P-ABCD中,底面ABCD为菱形,∠DAB=60°,平面PCD⊥底面ABCD,E是AB的中点,G为PA上的一点.
如图,四棱锥P-ABCD中,底面ABCD为菱形,∠DAB=60°,平面PCD⊥底面ABCD,E是AB的中点,G为PA上的一点.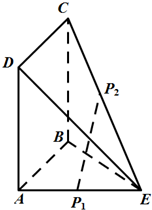 正方形ABCD的边长为1,AE=1,DE=
正方形ABCD的边长为1,AE=1,DE=