题目内容
已知曲线C1的极坐标方程是ρcos(θ+
)=2
.以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,曲线C2的参数方程是:
(t是参数).
(1)将曲线C1和曲线C2的方程转化为普通方程;
(2)若曲线C1与曲线C2相交于A、B两点,求证OA⊥OB;
(3)设直线y=kx+b与曲线C2交于两点P(x1,y1),Q(x2,y2),且|y1-y2|=a(a>0且a为常数),过弦PQ的中点M作平行于x轴的直线交曲线C2于点D,求证:△PQD的面积是定值.
| π |
| 4 |
| 2 |
|
(1)将曲线C1和曲线C2的方程转化为普通方程;
(2)若曲线C1与曲线C2相交于A、B两点,求证OA⊥OB;
(3)设直线y=kx+b与曲线C2交于两点P(x1,y1),Q(x2,y2),且|y1-y2|=a(a>0且a为常数),过弦PQ的中点M作平行于x轴的直线交曲线C2于点D,求证:△PQD的面积是定值.
考点:直线与圆锥曲线的关系,点的极坐标和直角坐标的互化,参数方程化成普通方程
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)利用极坐标方程与直角坐标方程的互化方法,参数方程消去参数,即可得到结论;
(2)联立曲线C1和曲线C2的方程并消元,利用向量的数量积公式,即可证明OA⊥OB;
(3)直线与抛物线联立,求出PQ中点M的坐标,D的坐标,即可证明:△PQD的面积是定值.
(2)联立曲线C1和曲线C2的方程并消元,利用向量的数量积公式,即可证明OA⊥OB;
(3)直线与抛物线联立,求出PQ中点M的坐标,D的坐标,即可证明:△PQD的面积是定值.
解答:
(1)解:曲线C1和曲线C2的方程转化为普通方程为C1:x-y-4=0,C2:y2=4x;
(2)证明:设A(x1,y1),B(x2,y2),联立曲线C1和曲线C2的方程并消元得:y2-4y-16=0,
∴y1+y2=4,
∴y1y2=-16,
∴
•
=x1x2+y1y2=(y1+4)(y2+4)+y1y2=0,
∴OA⊥OB.
(3)证明:
,消x得ky2-4y+4b=0,
∴y1+y2=
,y1y2=
,
由|y1-y2|=a(a>0且a为常数),得(y1+y2)2-4y1y2=a2,
∴a2k2=16(1-kb).
又可得PQ中点M的坐标为(
,
)=(
,
),
∴点D(
,
),
∴S△PQD=
DM•|y1-y2|=
•
•a=
.面积是定值.
(2)证明:设A(x1,y1),B(x2,y2),联立曲线C1和曲线C2的方程并消元得:y2-4y-16=0,
∴y1+y2=4,
∴y1y2=-16,
∴
| OA |
| OB |
∴OA⊥OB.
(3)证明:
|
∴y1+y2=
| 4 |
| k |
| 4b |
| k |
由|y1-y2|=a(a>0且a为常数),得(y1+y2)2-4y1y2=a2,
∴a2k2=16(1-kb).
又可得PQ中点M的坐标为(
| x1+x2 |
| 2 |
| y1+y2 |
| 2 |
| 2-bk |
| k2 |
| 2 |
| k |
∴点D(
| 1 |
| k2 |
| 2 |
| k |
∴S△PQD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1-bk |
| k2 |
| a3 |
| 32 |
点评:本题考查直线与圆锥曲线的关系、参数方程化成普通方程,考查学生分析解决问题的能力,难度中等.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
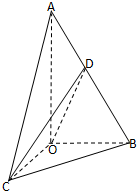 如图,在三棱锥A-BOC中,∠OAB=30°,AO⊥平面BOC,AB=4,∠BOC=90°,BO=CO,D是AB的中点.
如图,在三棱锥A-BOC中,∠OAB=30°,AO⊥平面BOC,AB=4,∠BOC=90°,BO=CO,D是AB的中点.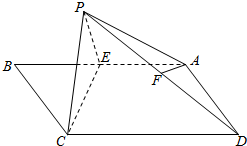 如图,在矩形ABCD中,AB=2,BC=1,E为AB的中点,以直线CE为折线将点B折起至点P,并保持∠PEB为锐角,连接PA,PC,PD,取PD的中点F.
如图,在矩形ABCD中,AB=2,BC=1,E为AB的中点,以直线CE为折线将点B折起至点P,并保持∠PEB为锐角,连接PA,PC,PD,取PD的中点F.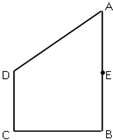 如图所示,在直角梯形ABCD中,E是AB的中点,∠B=∠C=90°,
如图所示,在直角梯形ABCD中,E是AB的中点,∠B=∠C=90°,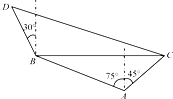 在海岸A处,发现北偏西75°的方向,与A距离2海里的B处有一艘走私船,在A处北偏东45°方向,与A距离(
在海岸A处,发现北偏西75°的方向,与A距离2海里的B处有一艘走私船,在A处北偏东45°方向,与A距离( 设抛物线C:y2=2px(p>0)的焦点为F,直线l过F且与抛物线C交于M、N两点,已知直线l与x轴垂直时,△OMN的面积为2(O为坐标原点).
设抛物线C:y2=2px(p>0)的焦点为F,直线l过F且与抛物线C交于M、N两点,已知直线l与x轴垂直时,△OMN的面积为2(O为坐标原点). 如图,AB是底面半径为1的圆柱的一条母线,O为下底面中心,BC是下底面的一条切线.
如图,AB是底面半径为1的圆柱的一条母线,O为下底面中心,BC是下底面的一条切线. 如图,已知四棱锥P-ABCD底面ABCD为矩形.PA=AD,侧面PAD垂直于底面ABCD,E是PD的中点.
如图,已知四棱锥P-ABCD底面ABCD为矩形.PA=AD,侧面PAD垂直于底面ABCD,E是PD的中点.