题目内容
 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为平行四边形,AB=1,AC=1,BC=
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为平行四边形,AB=1,AC=1,BC=| 2 |
(Ⅰ)证明:PC⊥平面ABE;
(Ⅱ)若∠PDC的大小为60度,求二面角B-AE-D的大小.
考点:与二面角有关的立体几何综合题,直线与平面垂直的判定
专题:空间角
分析:(Ⅰ)连结AC,由已知条件推导出AB⊥平面PAC,从而得到AB⊥PC,再由AE⊥PC,能证明PC⊥平面ABE.
(Ⅱ)以A为原点,AB为x轴,AC为y轴,AP为z轴,建立空间直角坐标系,利用向量法能求出二面角B-AE-D的大小.
(Ⅱ)以A为原点,AB为x轴,AC为y轴,AP为z轴,建立空间直角坐标系,利用向量法能求出二面角B-AE-D的大小.
解答:
 (Ⅰ)证明:连结AC,∵PA⊥平面ABCD,
(Ⅰ)证明:连结AC,∵PA⊥平面ABCD,
AB?平面ABCD,AC?平面ABCD,
∴PA⊥AB,PA⊥AC,
∵四边形ABCD为平行四边形,AB=1,AC=1,BC=
,
∴AB⊥AC,
∵PA∩AC=A,∴AB⊥平面PAC,
∵PC?平面PAC,∴AB⊥PC,
∵点E在PC上,AE⊥PC,
∵AB∩AE=A,∴PC⊥平面ABE.
(Ⅱ)解:以A为原点,AB为x轴,AC为y轴,AP为z轴,
建立空间直角坐标系,
∵AB=1,AC=1,BC=
,∠PDC=60°,
∴PD=2,PC=
,PA=
,
∴A(0,0,0),B(1,0,0),P(0,0,
),
C(0,1,0),D(-1,1,0),
∴
=(1,0,0),
=(-1,1,0),
=(0,1,-
),
设
=λ
=(0,λ,-
λ),则E(0,λ,
-
λ),
∴
=(0,λ,
-
λ),
∵AE⊥PC,∴
•
=λ-2+2λ=0,解得λ=
.∴
=(0,
,
),
设平面ABE的法向量
=(x,y,z),
则
,取z=
,得
=(0,-1,
).
设平面AED的法向量
=(x1,y1,z1),
则
,取x1=1,得
=(1,1,-
),
设二面角B-AE-D的平面角为θ,
则cosθ=-|cos<
,
>|=-|
|=-
.
∴θ=150°.
∴二面角B-AE-D的大小为150°.
 (Ⅰ)证明:连结AC,∵PA⊥平面ABCD,
(Ⅰ)证明:连结AC,∵PA⊥平面ABCD,AB?平面ABCD,AC?平面ABCD,
∴PA⊥AB,PA⊥AC,
∵四边形ABCD为平行四边形,AB=1,AC=1,BC=
| 2 |
∴AB⊥AC,
∵PA∩AC=A,∴AB⊥平面PAC,
∵PC?平面PAC,∴AB⊥PC,
∵点E在PC上,AE⊥PC,
∵AB∩AE=A,∴PC⊥平面ABE.
(Ⅱ)解:以A为原点,AB为x轴,AC为y轴,AP为z轴,
建立空间直角坐标系,
∵AB=1,AC=1,BC=
| 2 |
∴PD=2,PC=
| 3 |
| 2 |
∴A(0,0,0),B(1,0,0),P(0,0,
| 2 |
C(0,1,0),D(-1,1,0),
∴
| AB |
| AD |
| PC |
| 2 |
设
| PE |
| PC |
| 2 |
| 2 |
| 2 |
∴
| AE |
| 2 |
| 2 |
∵AE⊥PC,∴
| AE |
| PC |
| 2 |
| 3 |
| AE |
| 2 |
| 3 |
| ||
| 3 |
设平面ABE的法向量
| n |
则
|
| 2 |
| n |
| 2 |
设平面AED的法向量
| m |
则
|
| m |
| 2 |
设二面角B-AE-D的平面角为θ,
则cosθ=-|cos<
| n |
| m |
| 0-1-2 | ||||
|
| ||
| 2 |
∴θ=150°.
∴二面角B-AE-D的大小为150°.
点评:本题考查直线与平面垂直的证明,考查二面角的大小的求法,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
相关题目
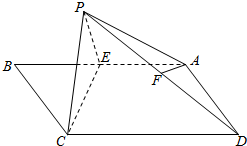 如图,在矩形ABCD中,AB=2,BC=1,E为AB的中点,以直线CE为折线将点B折起至点P,并保持∠PEB为锐角,连接PA,PC,PD,取PD的中点F.
如图,在矩形ABCD中,AB=2,BC=1,E为AB的中点,以直线CE为折线将点B折起至点P,并保持∠PEB为锐角,连接PA,PC,PD,取PD的中点F.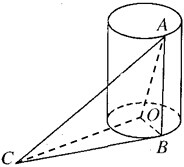 如图,AB是底面半径为1的圆柱的一条母线,O为下底面中心,BC是下底面的一条切线.
如图,AB是底面半径为1的圆柱的一条母线,O为下底面中心,BC是下底面的一条切线. 如图,已知四棱锥P-ABCD底面ABCD为矩形.PA=AD,侧面PAD垂直于底面ABCD,E是PD的中点.
如图,已知四棱锥P-ABCD底面ABCD为矩形.PA=AD,侧面PAD垂直于底面ABCD,E是PD的中点.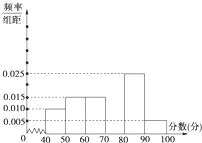 某中学团委组织了“弘扬奥运精神,爱我中华”的知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后画出如图所示部分频率分布直方图.观察图形给出的信息,回答下列问题:
某中学团委组织了“弘扬奥运精神,爱我中华”的知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后画出如图所示部分频率分布直方图.观察图形给出的信息,回答下列问题: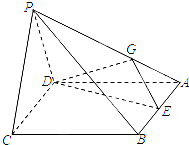 如图,四棱锥P-ABCD中,底面ABCD为菱形,∠DAB=60°,平面PCD⊥底面ABCD,E是AB的中点,G为PA上的一点.
如图,四棱锥P-ABCD中,底面ABCD为菱形,∠DAB=60°,平面PCD⊥底面ABCD,E是AB的中点,G为PA上的一点.