题目内容
已知点C(1,-2),P(-5,-2),动点满足|
|=3.
(1)求动点Q的轨迹方程;
(2)求
与
夹角的取值范围;
(3)是否存在斜率为1的直线l,l被点Q的轨迹所截得的弦为AB,以AB为直径的圆过原点?若存在,求出l的方程,若不存在,说明理由.
| QC |
(1)求动点Q的轨迹方程;
(2)求
| PC |
| PQ |
(3)是否存在斜率为1的直线l,l被点Q的轨迹所截得的弦为AB,以AB为直径的圆过原点?若存在,求出l的方程,若不存在,说明理由.
考点:直线与圆锥曲线的综合问题,轨迹方程
专题:圆锥曲线中的最值与范围问题
分析:(1)设点Q(x,y),由|
|=3,得
=3,由此能求出动点Q的轨迹方程.
(2)过P作圆C的切线,切点E,F,由EC=3,PC=6,由此能求出
与
夹角的取值范围.
(3)设l:y=x+t,由
,得2x2+(2+2t)x+t2+4t-4=0,设A(x1,y1),B(x2,y2),由此利用韦达定理、向量垂直结合已知条件能求出直线l的方程.
| QC |
| (x-1)2+(y+2)2 |
(2)过P作圆C的切线,切点E,F,由EC=3,PC=6,由此能求出
| PC |
| PQ |
(3)设l:y=x+t,由
|
解答:
解:(1)设点Q(x,y),由|
|=3,得
=3,
整理,得动点Q的轨迹方程为:
(x-1)2+(y+2)2=9.…(3分)
(2)过P作圆C的切线,切点E,F,
则EC=3,PC=6,
∴∠EPC=30°,
∴求
与
夹角的取值范围为[0,30°].…(8分)
(3)设这样的l存在,设l:y=x+t,
由
,
得2x2+(2+2t)x+t2+4t-4=0,※…(9分)
设A(x1,y1),B(x2,y2),
则x1+x2=-(t+1),x1x2=
,(10分)
由题设,
⊥
,
∴
•
=0,即x1x2+y1y2=0.(11分)
∵y1y2=(x1+t)(x2+t)=x1x2+t(x1+x2)+t2,(12分)
∴x1x2+y1y2=2x1x2+t(x1+x2)+t2=0,
整理,得t2+3t-4=0,(13分)
解得t=-4或t=1,
∴存在直线l:y=x-4或y=x+1.(14分)
| QC |
| (x-1)2+(y+2)2 |
整理,得动点Q的轨迹方程为:
(x-1)2+(y+2)2=9.…(3分)

(2)过P作圆C的切线,切点E,F,
则EC=3,PC=6,
∴∠EPC=30°,
∴求
| PC |
| PQ |
(3)设这样的l存在,设l:y=x+t,
由
|
得2x2+(2+2t)x+t2+4t-4=0,※…(9分)
设A(x1,y1),B(x2,y2),
则x1+x2=-(t+1),x1x2=
| t2+4t-4 |
| 2 |
由题设,
| OA |
| OB |
∴
| OA |
| OB |
∵y1y2=(x1+t)(x2+t)=x1x2+t(x1+x2)+t2,(12分)
∴x1x2+y1y2=2x1x2+t(x1+x2)+t2=0,
整理,得t2+3t-4=0,(13分)
解得t=-4或t=1,
∴存在直线l:y=x-4或y=x+1.(14分)
点评:本题考查点的轨迹方程的求法,考查向量的夹角的取值范围的求法,考查直线方程的求法,解题时要认真审题,注意向量垂直的条件的合理运用,

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
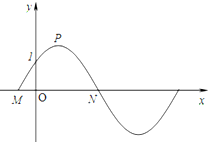 已知如图,函数y=2sin(
已知如图,函数y=2sin( 设抛物线C:y2=2px(p>0)的焦点为F,直线l过F且与抛物线C交于M、N两点,已知直线l与x轴垂直时,△OMN的面积为2(O为坐标原点).
设抛物线C:y2=2px(p>0)的焦点为F,直线l过F且与抛物线C交于M、N两点,已知直线l与x轴垂直时,△OMN的面积为2(O为坐标原点). 如图,已知四棱锥P-ABCD底面ABCD为矩形.PA=AD,侧面PAD垂直于底面ABCD,E是PD的中点.
如图,已知四棱锥P-ABCD底面ABCD为矩形.PA=AD,侧面PAD垂直于底面ABCD,E是PD的中点.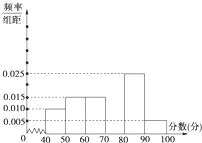 某中学团委组织了“弘扬奥运精神,爱我中华”的知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后画出如图所示部分频率分布直方图.观察图形给出的信息,回答下列问题:
某中学团委组织了“弘扬奥运精神,爱我中华”的知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后画出如图所示部分频率分布直方图.观察图形给出的信息,回答下列问题: 正方形ABCD的边长为1,AE=1,DE=
正方形ABCD的边长为1,AE=1,DE=