题目内容
已知函数f(x)=2sin(
x-
),x∈R,
(1)求f(
)的值;
(2)设α,β∈[0,
],f(2α+
)=
,f(2β+
)=
,α,β∈[0,
],求cos(α+β)的值.
| 1 |
| 2 |
| π |
| 3 |
(1)求f(
| 5π |
| 3 |
(2)设α,β∈[0,
| π |
| 2 |
| 2π |
| 3 |
| 10 |
| 13 |
| 5π |
| 3 |
| 6 |
| 5 |
| π |
| 2 |
考点:运用诱导公式化简求值
专题:三角函数的求值
分析:(1)将x=
代入f(x)计算即可求出所求式子的值;
(2)由已知两等式,根据f(x)解析式,求出sinα与cosβ的值,进而确定出cosα与sinβ的值,原式利用两角和与差的余弦函数公式化简,将各自的值代入计算即可求出值.
| 5π |
| 3 |
(2)由已知两等式,根据f(x)解析式,求出sinα与cosβ的值,进而确定出cosα与sinβ的值,原式利用两角和与差的余弦函数公式化简,将各自的值代入计算即可求出值.
解答:
解:(1)∵f(x)=2sin(
x-
),
∴f(
)=2sin(
×
-
)=2sin(
-
)=2sin
=2;
(2)∵f(2α+
)=2sin[
(2α+
)-
]=2sinα=
,
∴sinα=
,
∵f(2β+
)=2sin[
(2β+
)-
]=2sin(β+
)=2cosβ=
,
∴cosβ=
,
∵α,β∈[0,
],
∴cosα=
,sinβ=
,
则cos(α+β)=cosαcosβ-sinαsinβ=
×
-
×
=
.
| 1 |
| 2 |
| π |
| 3 |
∴f(
| 5π |
| 3 |
| 1 |
| 2 |
| 5π |
| 3 |
| π |
| 3 |
| 5π |
| 6 |
| π |
| 3 |
| π |
| 2 |
(2)∵f(2α+
| 2π |
| 3 |
| 1 |
| 2 |
| 2π |
| 3 |
| π |
| 3 |
| 10 |
| 13 |
∴sinα=
| 5 |
| 13 |
∵f(2β+
| 5π |
| 3 |
| 1 |
| 2 |
| 5π |
| 3 |
| π |
| 3 |
| π |
| 2 |
| 6 |
| 5 |
∴cosβ=
| 3 |
| 5 |
∵α,β∈[0,
| π |
| 2 |
∴cosα=
| 12 |
| 13 |
| 4 |
| 5 |
则cos(α+β)=cosαcosβ-sinαsinβ=
| 12 |
| 13 |
| 3 |
| 5 |
| 5 |
| 13 |
| 4 |
| 5 |
| 16 |
| 65 |
点评:此题考查了运用诱导公式化简求值,熟练掌握诱导公式是解本题的关键.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
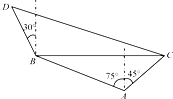 在海岸A处,发现北偏西75°的方向,与A距离2海里的B处有一艘走私船,在A处北偏东45°方向,与A距离(
在海岸A处,发现北偏西75°的方向,与A距离2海里的B处有一艘走私船,在A处北偏东45°方向,与A距离(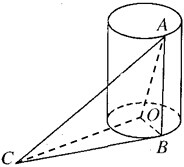 如图,AB是底面半径为1的圆柱的一条母线,O为下底面中心,BC是下底面的一条切线.
如图,AB是底面半径为1的圆柱的一条母线,O为下底面中心,BC是下底面的一条切线.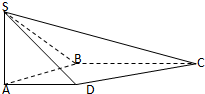 如图,在四棱锥S-ABCD中,SA⊥平面ABCD,底面ABCD为直角梯形,AD∥BC,∠ABC=90°,SA=AB=1,
如图,在四棱锥S-ABCD中,SA⊥平面ABCD,底面ABCD为直角梯形,AD∥BC,∠ABC=90°,SA=AB=1, 如图,已知四棱锥P-ABCD底面ABCD为矩形.PA=AD,侧面PAD垂直于底面ABCD,E是PD的中点.
如图,已知四棱锥P-ABCD底面ABCD为矩形.PA=AD,侧面PAD垂直于底面ABCD,E是PD的中点.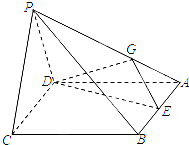 如图,四棱锥P-ABCD中,底面ABCD为菱形,∠DAB=60°,平面PCD⊥底面ABCD,E是AB的中点,G为PA上的一点.
如图,四棱锥P-ABCD中,底面ABCD为菱形,∠DAB=60°,平面PCD⊥底面ABCD,E是AB的中点,G为PA上的一点.