题目内容
在平面直角坐标系xoy中,以原点O为圆心的圆O是曲线|x|+|y|=
的内切圆.
(1)求圆O的方程;
(2)若直线l与圆O相切于第一象限,且与x、y轴分别交于D,E两点,当DE长最小时,求直线l的方程;
(3)设M,P是圆O上任意两点,点M关于x轴的对称点为N,若直线MP、NP分别交于x轴于点A(m,0)和B(n,0),问这两点的横坐标之积mn是否为定值?若是,请求出该定值;若不是,请说明理由.
| 6 |
(1)求圆O的方程;
(2)若直线l与圆O相切于第一象限,且与x、y轴分别交于D,E两点,当DE长最小时,求直线l的方程;
(3)设M,P是圆O上任意两点,点M关于x轴的对称点为N,若直线MP、NP分别交于x轴于点A(m,0)和B(n,0),问这两点的横坐标之积mn是否为定值?若是,请求出该定值;若不是,请说明理由.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)由已知条件推导出曲线是由(
,0),(0,
),(-
,0),(0,-
)围成的正方形,由此能求出圆O的方程.
(2)设直线l与圆O的切点为(x0,y0),则直线lx0x+y0y=3,令f(x0)=x02(3-x02)=-(x02)2+3x02,由已知条件推导出x0=
时,f(x0)最大,由此能求出直线l的方程.
(3)设P(x1,y1),M(x2,y2),直线PM的方程:y-y1=
(x-x1),从而解得A(
,0),B(
,0),由此能求出mn=3.
| 6 |
| 6 |
| 6 |
| 6 |
(2)设直线l与圆O的切点为(x0,y0),则直线lx0x+y0y=3,令f(x0)=x02(3-x02)=-(x02)2+3x02,由已知条件推导出x0=
| ||
| 2 |
(3)设P(x1,y1),M(x2,y2),直线PM的方程:y-y1=
| y2-y1 |
| x2-x1 |
| x1y2-x2y1 |
| y2-y1 |
| x1y2+x2y1 |
| y2+y1 |
解答:
解:(1)当x≥0,y≥0时,
曲线x+y=
是以点(
,0),(0,
)为端点的线段,
根据对称性可知,曲线是由(
,0),(0,
),(-
,0),(0,-
)围成的正方形,
∴圆O的半径
,∴圆O的方程为x2+y2=3.
(2)设直线l与圆O的切点为(x0,y0),则x02+y02=3,(x0>0,y0>0),
∴直线l:y-y0=-
(x-x0),即x0x+y0y=3,
∴D(
,0),E(0,
),
∴DE=
=
,
令f(x0)=x02(3-x02)=-(x02)2+3x02,
∴x02=
,即x0=
时,f(x0)最大,
此时DE最大,y0=
,∴直线l:x0+y0=
.
(3)设P(x1,y1),M(x2,y2),
则N(x2,-y2),x12+y12=3,x22+y22=3,
∴直线PM的方程:y-y1=
(x-x1),
令y=0,解得A(
,0),同理B(
,0),
∴mn=
•
=
=
=3.
曲线x+y=
| 6 |
| 6 |
| 6 |
根据对称性可知,曲线是由(
| 6 |
| 6 |
| 6 |
| 6 |
∴圆O的半径
| 3 |
(2)设直线l与圆O的切点为(x0,y0),则x02+y02=3,(x0>0,y0>0),
∴直线l:y-y0=-
| x0 |
| y0 |
∴D(
| 3 |
| x0 |
| 3 |
| y0 |
∴DE=
|
3
| ||
|
令f(x0)=x02(3-x02)=-(x02)2+3x02,
∴x02=
| 3 |
| 2 |
| ||
| 2 |
此时DE最大,y0=
| ||
| 2 |
| 6 |
(3)设P(x1,y1),M(x2,y2),
则N(x2,-y2),x12+y12=3,x22+y22=3,
∴直线PM的方程:y-y1=
| y2-y1 |
| x2-x1 |
令y=0,解得A(
| x1y2-x2y1 |
| y2-y1 |
| x1y2+x2y1 |
| y2+y1 |
∴mn=
| x1y2-x2y1 |
| y2-y1 |
| x1y2+x2y1 |
| y2+y1 |
| x12y22-x22y12 |
| y22-y12 |
| (3-y12)y22-(3-y22)y12 |
| y22-y12 |
点评:本题考查圆的方程的求法,考查直线方程的求法,考查两点横坐标之积是否为定值的判断与求法,解题时要认真审题,注意函数与方程思想的合理运用.

练习册系列答案
相关题目
 如图,已知四棱锥P-ABCD底面ABCD为矩形.PA=AD,侧面PAD垂直于底面ABCD,E是PD的中点.
如图,已知四棱锥P-ABCD底面ABCD为矩形.PA=AD,侧面PAD垂直于底面ABCD,E是PD的中点.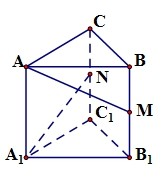 13、如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=2,AA1=4,若M,N分别是BB1,CC1的中点,则异面直线AM与A1N所成的角的大小为
13、如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=2,AA1=4,若M,N分别是BB1,CC1的中点,则异面直线AM与A1N所成的角的大小为