题目内容
实数m取什么值时,复数z=m(m+2)+(m2-4)i(i是虚数单位):
(1)是虚数;
(2)是纯虚数;
(3)在复平面内对应的点在第四象限.
(1)是虚数;
(2)是纯虚数;
(3)在复平面内对应的点在第四象限.
考点:复数的基本概念,复数的代数表示法及其几何意义
专题:数系的扩充和复数
分析:(1)由复数z=m(m+2)+(m2-4)i(i是虚数单位)是虚数,可得m2-4≠0,解得m即可.
(2)由复数z=m(m+2)+(m2-4)i(i是虚数单位)是纯虚数,可得
,解得m即可.
(3)由复数z=m(m+2)+(m2-4)i(i是虚数单位)在复平面内对应的点在第四象限.
可得
,解得即可.
(2)由复数z=m(m+2)+(m2-4)i(i是虚数单位)是纯虚数,可得
|
(3)由复数z=m(m+2)+(m2-4)i(i是虚数单位)在复平面内对应的点在第四象限.
可得
|
解答:
解:(1)∵复数z=m(m+2)+(m2-4)i(i是虚数单位)是虚数,∴m2-4≠0,解得m≠±2.
(2)∵复数z=m(m+2)+(m2-4)i(i是虚数单位)是纯虚数,∴
,解得m=0.
(3)∵复数z=m(m+2)+(m2-4)i(i是虚数单位)在复平面内对应的点在第四象限.
∴
,解得0<m<2.
(2)∵复数z=m(m+2)+(m2-4)i(i是虚数单位)是纯虚数,∴
|
(3)∵复数z=m(m+2)+(m2-4)i(i是虚数单位)在复平面内对应的点在第四象限.
∴
|
点评:本题考查了虚数、纯虚数的定义及其复数的几何意义,属于基础题.

练习册系列答案
相关题目
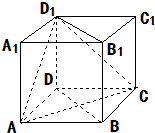 如图,在正方体ABCD-A1B1C1D1中.求证:平面ACD1⊥平面BB1D1D.
如图,在正方体ABCD-A1B1C1D1中.求证:平面ACD1⊥平面BB1D1D.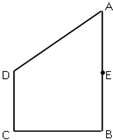 如图所示,在直角梯形ABCD中,E是AB的中点,∠B=∠C=90°,
如图所示,在直角梯形ABCD中,E是AB的中点,∠B=∠C=90°, 设抛物线C:y2=2px(p>0)的焦点为F,直线l过F且与抛物线C交于M、N两点,已知直线l与x轴垂直时,△OMN的面积为2(O为坐标原点).
设抛物线C:y2=2px(p>0)的焦点为F,直线l过F且与抛物线C交于M、N两点,已知直线l与x轴垂直时,△OMN的面积为2(O为坐标原点).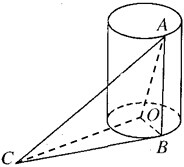 如图,AB是底面半径为1的圆柱的一条母线,O为下底面中心,BC是下底面的一条切线.
如图,AB是底面半径为1的圆柱的一条母线,O为下底面中心,BC是下底面的一条切线. 如图,已知四棱锥P-ABCD底面ABCD为矩形.PA=AD,侧面PAD垂直于底面ABCD,E是PD的中点.
如图,已知四棱锥P-ABCD底面ABCD为矩形.PA=AD,侧面PAD垂直于底面ABCD,E是PD的中点.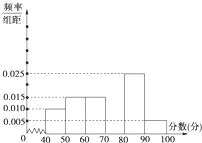 某中学团委组织了“弘扬奥运精神,爱我中华”的知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后画出如图所示部分频率分布直方图.观察图形给出的信息,回答下列问题:
某中学团委组织了“弘扬奥运精神,爱我中华”的知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后画出如图所示部分频率分布直方图.观察图形给出的信息,回答下列问题: