题目内容
已知抛物线的顶点在坐标原点O，焦点F在x轴上，抛物线上的点A到F的距离为2，且A的横坐标为l．直线l：y=kx+b与抛物线交于B，C两点．
（1）求抛物线的方程；
（2）当直线OB，OC的倾斜角之和为45°时，证明直线l过定点．
（1）求抛物线的方程；
（2）当直线OB，OC的倾斜角之和为45°时，证明直线l过定点．
考点：直线与圆锥曲线的综合问题
专题：综合题,圆锥曲线的定义、性质与方程
分析：（1）设抛物线方程为y2=2px，由抛物线上的点A到F的距离为2，且A的横坐标为l，利用抛物线的定义，求出p，即可得到抛物线的方程；
（2）直线l：y=kx+b与抛物线联立，设直线OB，OC的倾斜角分别为α，β，斜率分别为k1，k2，则α+β=45°，利用tan（α+β）=
=tan45°=1，代入斜率，可得直线l的方程为y=kx+4k+4，即可得出直线l过定点．
（2）直线l：y=kx+b与抛物线联立，设直线OB，OC的倾斜角分别为α，β，斜率分别为k1，k2，则α+β=45°，利用tan（α+β）=
| k1+k2 |
| 1-k1k2 |
解答：
（1）解：设抛物线方程为y2=2px（p＞0
由抛物线的定义知|AF|=1+
，又|AF|=2…（2分）
所以p=2，所以抛物线 的方程为y2=4x…（4分）
（2）证明：设B（
，y1），C（
，y2）
联立
，整理得ky2-4y+4b=0（依题意k≠0），
y1+y2=
，y1y2=
．…（6分）
设直线OB，OC的倾斜角分别为α，β，斜率分别为k1，k2，则α+β=45°，
tan（α+β）=
=tan45°=1，…（8分）
其中k1=
=
，k2=
，代入上式整理得y1y2-16-（y1+y2）=0
所以
-16=
，即b=4k+4…（10分）
直线l的方程为y=kx+4k+4，整理得y-4=k（x+4），
所以直线l过定点（-4，4）…（12分）
由抛物线的定义知|AF|=1+
| p |
| 2 |
所以p=2，所以抛物线 的方程为y2=4x…（4分）
（2）证明：设B（
| ||
| 4 |
| ||
| 4 |
联立
|
y1+y2=
| 4 |
| k |
| 4b |
| k |
设直线OB，OC的倾斜角分别为α，β，斜率分别为k1，k2，则α+β=45°，
tan（α+β）=
| k1+k2 |
| 1-k1k2 |
其中k1=
| y1 |
| x1 |
| 4 |
| y1 |
| 4 |
| y2 |
所以
| 4b |
| k |
| 16 |
| k |
直线l的方程为y=kx+4k+4，整理得y-4=k（x+4），
所以直线l过定点（-4，4）…（12分）
点评：本题考查椭圆的方程，考查直线与椭圆的位置关系，考查韦达定理的运用，考查和角的正切公式，考查学生的计算能力，属于中档题．
练习册系列答案
相关题目
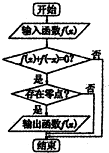
某流程图如图所示，现输入如下四个函数，则可以输出的函数是（ ）
| A、f（x）=x2-1 | ||
B、f（x）=
| ||
C、f（x）=
| ||
| D、f（x）=3sinx+1 |
“m=1”是“复数z=（1+mi）（1+i）（m∈R，i为虚数单位）为纯虚数”的（ ）
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
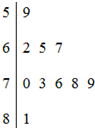已知某山区小学有100名四年级学生，将全体四年级学生随机按00～99编号，并且按编号顺序平均分成10组．现要从中抽取10名学生，各组内抽取的编号按依次增加10进行系统抽样．