题目内容
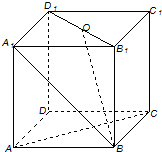在正方体ABCD-A1B1C1D1中，O为B1D1的中点，则AC与DD1所成的角为考点：异面直线及其所成的角
专题：空间角
分析：利用正方体的性质、异面直线所成角的概念、余弦定理求解．
解答：
解：在正方体ABCD-A1B1C1D1中，O为B1D1的中点，
∵DD1⊥平面ABCD，AC?平面ABCD，∴DD1⊥AC，
故AC与DD1所成的角为90°；
∵D1C1∥DC，
∴AC与D1C1所成的角为∠ACD，
∵∠ACD=45°，∴AC与D1C1所成的角为45°；
∵B1D1∥BD，AC⊥BD，∴AC⊥B1D1，
∴AC与B1D1所成角为90°；
∵AC∥A1C1，∴AC与A1B所成的角为∠BA1C1，
∵△BA1C1是等边三角形，∴AC与A1B所成的角为60°；
∵BD∥B1D1，∴A1B与B1D1所成的角为∠A1BD，
∵△A1BD为等边三角形，
∴∠A1BD=60°，
∴A1B与B1D1所成角为60°；
∵AC∥A1O，∴∠A1OB是AC与BO所成的角，
设正方体的棱长为1，则A1O=
，BO=
=
，A1B=
，
∴cos∠A1OB=
=
=-
．
∴AC与BO所成的角为π-arccos
．
∵DD1⊥平面ABCD，AC?平面ABCD，∴DD1⊥AC，
故AC与DD1所成的角为90°；
∵D1C1∥DC，
∴AC与D1C1所成的角为∠ACD，
∵∠ACD=45°，∴AC与D1C1所成的角为45°；
∵B1D1∥BD，AC⊥BD，∴AC⊥B1D1，
∴AC与B1D1所成角为90°；
∵AC∥A1C1，∴AC与A1B所成的角为∠BA1C1，
∵△BA1C1是等边三角形，∴AC与A1B所成的角为60°；
∵BD∥B1D1，∴A1B与B1D1所成的角为∠A1BD，
∵△A1BD为等边三角形，
∴∠A1BD=60°，
∴A1B与B1D1所成角为60°；
∵AC∥A1O，∴∠A1OB是AC与BO所成的角，
设正方体的棱长为1，则A1O=
| ||
| 2 |
1+
|
| ||
| 2 |
| 2 |
∴cos∠A1OB=
| A1O2+BO2-AB2 |
| 2A1O•BO |
| ||||||||
2×
|
| ||
| 20 |
∴AC与BO所成的角为π-arccos
| ||
| 20 |
点评：本题考查异面直线所成的角的求法，是中档题，解题时要注意空间思维能力的培养．
练习册系列答案
名校课堂系列答案
相关题目
如图，已知在梯形ABCD中，AB∥CD，过D作与BC平行的直线交AB于点E，∠ACE=∠ABC，求证：AB•CE=AC•DE．