题目内容
定义域为R的偶函数f（x）满足：对任意的x∈R，都有f（x+2）=f（x），且当x∈[0，1〕，时f（x）=
，则函数g（x）=3f（x）-x，在R上的零点个数是（ ）
| x |
| A、0 | B、1 | C、2 | D、3 |
考点：根的存在性及根的个数判断
专题：计算题,作图题,函数的性质及应用
分析：函数g（x）=3f（x）-x在R上的零点个数可化为函数f（x）与函数h（x）=
交点的个数，作出图象，由图象得零点个数．
| x |
| 3 |
解答：
解：函数g（x）=3f（x）-x在R上的零点个数可化为
函数f（x）与函数h（x）=
交点的个数，
∵函数f（x）是R上周期为2的偶函数，且当x∈[0，1〕，时f（x）=
，
∴作出函数f（x）与函数h（x）=
的图象如下图：
由图可知，有三个不同的交点，
故选D．
函数f（x）与函数h（x）=
| x |
| 3 |
∵函数f（x）是R上周期为2的偶函数，且当x∈[0，1〕，时f（x）=
| x |
∴作出函数f（x）与函数h（x）=
| x |
| 3 |
由图可知，有三个不同的交点，
故选D．
点评：本题考查了学生的作图能力与画图能力，属于中档题．
练习册系列答案
相关题目
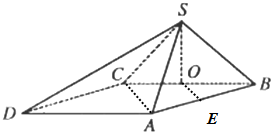四棱锥S-ABCD中，底面ABCD为平行四边形，且AC⊥AB，O，E分别为BC，AB的中点．已知∠ABC=45°，AB=2，BC=2
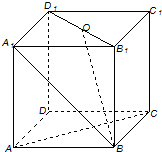在正方体ABCD-A1B1C1D1中，O为B1D1的中点，则AC与DD1所成的角为
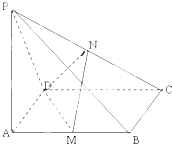如图，PA⊥平面ABCD，四边形ABCD是矩形，PA=AD，M，N分别是AB，PC的中点．