题目内容
已知函数f(x)=x2+2|x-a|(a>0),若f(x)在(-1,1)上的最小值为g(a).
(1)求g(a);
(2)证明:当x∈[-1,1]时,恒有f(x)≤g(a)+4.
(1)求g(a);
(2)证明:当x∈[-1,1]时,恒有f(x)≤g(a)+4.
考点:函数的最值及其几何意义
专题:计算题,证明题,函数的性质及应用
分析:(1)讨论去掉绝对值号,再讨论a的不同取值范围从而得到g(a);
(2)结合(1)可求f(x)在[-1,1]上的最大值,说明最大值不大于g(a)+4即可.
(2)结合(1)可求f(x)在[-1,1]上的最大值,说明最大值不大于g(a)+4即可.
解答:
解:(1)f(x)=x2+2|x-a|=
,
又∵a>0,
∴①0<a<1时,
g(a)=f(x)min=f(a)=a2;
②a≥1时,f(x)在(-1,1)上单调递减,无最小值;
综上所述,g(a)=a2,(0<a<1)
(2)证明:由(1)知,0<a<1,
又∵f(-1)=3+2a,f(1)=3-2a;
则f(x)≤3+2a,
又∵g(a)+4-(3+2a)=a2+4-(3+2a)=a2+1-2a=(a-1)2>0,
∴恒有f(x)≤g(a)+4.
|
又∵a>0,
∴①0<a<1时,
g(a)=f(x)min=f(a)=a2;
②a≥1时,f(x)在(-1,1)上单调递减,无最小值;
综上所述,g(a)=a2,(0<a<1)
(2)证明:由(1)知,0<a<1,
又∵f(-1)=3+2a,f(1)=3-2a;
则f(x)≤3+2a,
又∵g(a)+4-(3+2a)=a2+4-(3+2a)=a2+1-2a=(a-1)2>0,
∴恒有f(x)≤g(a)+4.
点评:本题考查了函数中绝对值符号的去除方法,同时考查了函数最值的求法及恒成立问题的证明,属于中档题.

练习册系列答案
相关题目
函数y=x-
,当x∈[1,4]时,函数的最大值与最小值的差是( )
| 4 |
| x |
| A、-6 | B、6 | C、3 | D、-3 |
 在四棱锥V-ABCD中,底面ABCD是正方形,侧面VAD是正三角形,平面VAD⊥底面ABCD.
在四棱锥V-ABCD中,底面ABCD是正方形,侧面VAD是正三角形,平面VAD⊥底面ABCD.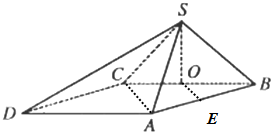 四棱锥S-ABCD中,底面ABCD为平行四边形,且AC⊥AB,O,E分别为BC,AB的中点.已知∠ABC=45°,AB=2,BC=2
四棱锥S-ABCD中,底面ABCD为平行四边形,且AC⊥AB,O,E分别为BC,AB的中点.已知∠ABC=45°,AB=2,BC=2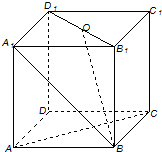 在正方体ABCD-A1B1C1D1中,O为B1D1的中点,则AC与DD1所成的角为
在正方体ABCD-A1B1C1D1中,O为B1D1的中点,则AC与DD1所成的角为