题目内容
已知数列{an}的首项a1=2,且对任意n∈N*,都有an+1=ban+c,其中b,c是常数.
(1)若数列{an}是等差数列,且c=2,求数列{an}的通项公式;
(2)若数列{an}是等比数列,且|b|<2,当从数列{an}中任意取出相邻的三项,按某种顺序排列成等差数列,求使数列{an}的前n项和Sn<
成立的n的取值集合.
(1)若数列{an}是等差数列,且c=2,求数列{an}的通项公式;
(2)若数列{an}是等比数列,且|b|<2,当从数列{an}中任意取出相邻的三项,按某种顺序排列成等差数列,求使数列{an}的前n项和Sn<
| 341 |
| 256 |
考点:数列的求和,等差数列的通项公式
专题:等差数列与等比数列,不等式的解法及应用
分析:(1)当c=2时,求出a2,a3的值,由等差数列的性质列式求出b,然后分类求出数列{an}的通项公式;
(2)由数列{an}是等比数列,根据等比数列的性质得到c=0或2b+c=2,当2b+c=2时不满足题意,当c=0时分b=0和b≠0讨论,当b≠0时由an,an+1,an+2按某种顺序排列成等差数列得到1+b=2b2,或1+b2=2b,或b+b2=2,结合b的范围求出b,代入等比数列的求和公式求解Sn<
得答案.
(2)由数列{an}是等比数列,根据等比数列的性质得到c=0或2b+c=2,当2b+c=2时不满足题意,当c=0时分b=0和b≠0讨论,当b≠0时由an,an+1,an+2按某种顺序排列成等差数列得到1+b=2b2,或1+b2=2b,或b+b2=2,结合b的范围求出b,代入等比数列的求和公式求解Sn<
| 341 |
| 256 |
解答:
解:(1)当c=2时,由已知得,
a1=2,a2=ba1+2=2b+2,a3=ba2+2=2b2+2b+2,
∵{an}是等差数列,
∴a1+a3=2a2,
即2+(2b2+2b+2)=2(2b+2),
∴b2-b=0,解得b=0或b=1.
当b=0时,an=2对n∈N*有an+1-an=0成立,
∴数列{an}是差数列;
当b=1时,an+1=an+2(n∈N*),即an+1-an=2成立,数列{an}是差数列.
∴数列{an}的通项公式分别为an=2或an=2n.
(2)∵{an}是等比数列,
∴a1a3=a22,
即2[b(2b+c)+c]=(2b+c)2,化简得2bc+c2=2c,
∴c=0或2b+c=2.
当2b+c=2时,a2=ba1+c=2b+c=2,an=2,不满足Sn<
;
当c=0时,若b=0,则a1=0,与a1=2矛盾,
∴b≠0,则an=2bn-1,
则an+1=2bn,an+2=2bn+1,
∵an,an+1,an+2按某种顺序排列成等差数列,
∴1+b=2b2,或1+b2=2b,或b+b2=2,
解之得b=1,-
,-2.
又∵|b|<2
∴b=-
,或b=1,
当b=-
时,
则Sn=
=
[1-(-
)n],
由Sn<
,得
[1-(-
)n]<
,即(-
)n>
.
∵n为正整数,
∴n取值集合为{2,4,6,8}.
当b=1时,Sn=2n,不合题意.
a1=2,a2=ba1+2=2b+2,a3=ba2+2=2b2+2b+2,
∵{an}是等差数列,
∴a1+a3=2a2,
即2+(2b2+2b+2)=2(2b+2),
∴b2-b=0,解得b=0或b=1.
当b=0时,an=2对n∈N*有an+1-an=0成立,
∴数列{an}是差数列;
当b=1时,an+1=an+2(n∈N*),即an+1-an=2成立,数列{an}是差数列.
∴数列{an}的通项公式分别为an=2或an=2n.
(2)∵{an}是等比数列,
∴a1a3=a22,
即2[b(2b+c)+c]=(2b+c)2,化简得2bc+c2=2c,
∴c=0或2b+c=2.
当2b+c=2时,a2=ba1+c=2b+c=2,an=2,不满足Sn<
| 341 |
| 256 |
当c=0时,若b=0,则a1=0,与a1=2矛盾,
∴b≠0,则an=2bn-1,
则an+1=2bn,an+2=2bn+1,
∵an,an+1,an+2按某种顺序排列成等差数列,
∴1+b=2b2,或1+b2=2b,或b+b2=2,
解之得b=1,-
| 1 |
| 2 |
又∵|b|<2
∴b=-
| 1 |
| 2 |
当b=-
| 1 |
| 2 |
则Sn=
2[1-(-
| ||
1-(-
|
| 4 |
| 3 |
| 1 |
| 2 |
由Sn<
| 341 |
| 256 |
| 4 |
| 3 |
| 1 |
| 2 |
| 341 |
| 256 |
| 1 |
| 2 |
| 1 |
| 1024 |
∵n为正整数,
∴n取值集合为{2,4,6,8}.
当b=1时,Sn=2n,不合题意.
点评:本题考查了等差数列和等比数列的通项公式,考查了等差数列的性质,考查了等比数列的前n项和,训练了数列不等式的解法,体现了分类讨论的首项思想方法,是压轴题.

练习册系列答案
相关题目
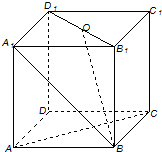 在正方体ABCD-A1B1C1D1中,O为B1D1的中点,则AC与DD1所成的角为
在正方体ABCD-A1B1C1D1中,O为B1D1的中点,则AC与DD1所成的角为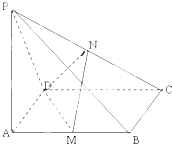 如图,PA⊥平面ABCD,四边形ABCD是矩形,PA=AD,M,N分别是AB,PC的中点.
如图,PA⊥平面ABCD,四边形ABCD是矩形,PA=AD,M,N分别是AB,PC的中点. 如图,已知正方体ABCD-A1B1C1D1的棱长为1,M、N分别是对角线AD1、BD上的点,且AM=BN=x.
如图,已知正方体ABCD-A1B1C1D1的棱长为1,M、N分别是对角线AD1、BD上的点,且AM=BN=x.