题目内容
已知数列{an}中,a1=
,an+1=
an+(
)n+1,求an.
| 5 |
| 6 |
| 1 |
| 3 |
| 1 |
| 2 |
考点:数列递推式
专题:等差数列与等比数列
分析:数列{an}中,a1=
,an+1=
an+(
)n+1,两边同时乘以3n+1,得3n+1an+1=3nan+(
)n+1,从而3n+1an+1-3ⁿan=(
)n+1,由此能求出数列{an}的通项公式.
| 5 |
| 6 |
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
解答:
解:∵数列{an}中,a1=
,an+1=
an+(
)n+1,
两边同时乘以3n+1,得3n+1an+1=3nan+(
)n+1,
从而3n+1an+1-3ⁿan=(
)n+1,
从而有:
3ⁿan-3n+1an-1=(
)ⁿ,
3n+1an-1-3n+2an-2=(
)n+1,
32a2-3a1=(
)2,
3a1=
,
累加得3ⁿan=3(
)ⁿ-2,
故an=
-
.
综上,数列{an}的通项公式为an=
-
.
| 5 |
| 6 |
| 1 |
| 3 |
| 1 |
| 2 |
两边同时乘以3n+1,得3n+1an+1=3nan+(
| 3 |
| 2 |
从而3n+1an+1-3ⁿan=(
| 3 |
| 2 |
从而有:
3ⁿan-3n+1an-1=(
| 3 |
| 2 |
3n+1an-1-3n+2an-2=(
| 3 |
| 2 |
32a2-3a1=(
| 3 |
| 2 |
3a1=
| 5 |
| 2 |
累加得3ⁿan=3(
| 3 |
| 2 |
故an=
| 3 |
| 2n |
| 2 |
| 3n |
综上,数列{an}的通项公式为an=
| 3 |
| 2n |
| 2 |
| 3n |
点评:本题考查数列的通项公式的求法,是中档题,解题时要认真审题,注意累加法的合理运用.

练习册系列答案
相关题目
函数y=x-
,当x∈[1,4]时,函数的最大值与最小值的差是( )
| 4 |
| x |
| A、-6 | B、6 | C、3 | D、-3 |
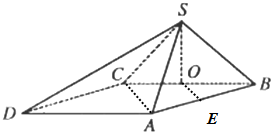 四棱锥S-ABCD中,底面ABCD为平行四边形,且AC⊥AB,O,E分别为BC,AB的中点.已知∠ABC=45°,AB=2,BC=2
四棱锥S-ABCD中,底面ABCD为平行四边形,且AC⊥AB,O,E分别为BC,AB的中点.已知∠ABC=45°,AB=2,BC=2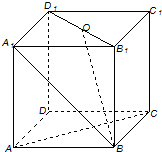 在正方体ABCD-A1B1C1D1中,O为B1D1的中点,则AC与DD1所成的角为
在正方体ABCD-A1B1C1D1中,O为B1D1的中点,则AC与DD1所成的角为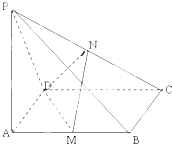 如图,PA⊥平面ABCD,四边形ABCD是矩形,PA=AD,M,N分别是AB,PC的中点.
如图,PA⊥平面ABCD,四边形ABCD是矩形,PA=AD,M,N分别是AB,PC的中点.