题目内容
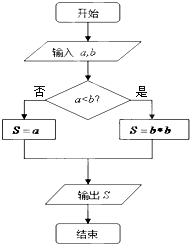 对于给定的实数a、b,定义运算“⊕”:s=a⊕b.若其运算法则如程序框图所示,则集合{y|y=(1⊕x)•x+(2⊕x),x∈[-2,2]}(注:“•”和“+”表示实数的乘法和加法运算)的最大元素是
对于给定的实数a、b,定义运算“⊕”:s=a⊕b.若其运算法则如程序框图所示,则集合{y|y=(1⊕x)•x+(2⊕x),x∈[-2,2]}(注:“•”和“+”表示实数的乘法和加法运算)的最大元素是考点:程序框图
专题:新定义
分析:根据程序框图知定义新运算“⊕”如下:当a≥b时,a⊕b=a;当a<b时,a⊕b=b2.再分类讨论,利用新定义,确定函数f(x)=(1⊕x)•x+(2⊕x)的解析式,利用函数的单调性,即可得到结论.
解答:
解:根据程序框图知,
①当-2≤x≤1时,∵当a≥b时,a⊕b=a,∴1⊕x=1,2⊕x=2
∴(1⊕x)x+(2⊕x)=x+2,∴当-2≤x≤1时,函数f(x)=(1⊕x)•x+(2⊕x)的最大值等于3;
②当1<x≤2时,∵当a<b时,a⊕b=b2,∴(1⊕x)x+(2⊕x)=x2•x+(2⊕x)=x3+(2⊕x)=x3+2,
∴当1<x≤2时,此函数当x=2时有最大值10.
综上知,函数f(x)=(1⊕x)•x+2⊕x)的最大值等于10.
即则集合{y|y=(1⊕x)•x+(2⊕x),x∈[-2,2]}的最大元素是10.
故答案为:10.
①当-2≤x≤1时,∵当a≥b时,a⊕b=a,∴1⊕x=1,2⊕x=2
∴(1⊕x)x+(2⊕x)=x+2,∴当-2≤x≤1时,函数f(x)=(1⊕x)•x+(2⊕x)的最大值等于3;
②当1<x≤2时,∵当a<b时,a⊕b=b2,∴(1⊕x)x+(2⊕x)=x2•x+(2⊕x)=x3+(2⊕x)=x3+2,
∴当1<x≤2时,此函数当x=2时有最大值10.
综上知,函数f(x)=(1⊕x)•x+2⊕x)的最大值等于10.
即则集合{y|y=(1⊕x)•x+(2⊕x),x∈[-2,2]}的最大元素是10.
故答案为:10.
点评:本题考查程序框图,新定义,考查分类讨论的数学思想,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
已知函数f(x)是定义在(-6,6)上的偶函数,f(x)在[0,6]上是单调函数,且f(-2)≤f(1),f(-2)=25,那么下列肯定不正确的是( )
| A、f(1)≥25 |
| B、f(2)=25 |
| C、f(1)<25 |
| D、f(1)>25 |
设函数f(x)(x∈R)满足f(x+2)=f(x)+2.当0≤x<2时,f(x)=1,则f(2014)=( )
| A、2013 | B、2014 |
| C、2015 | D、2016 |
若关于x的方程x2-2mx+m+6=0的两实根为x1,x2,y=(x1-1)2+(x2-1)2的取值范围是( )
A、y≥
| ||
| B、y≥8 | ||
| C、y≥18 | ||
D、y>-
|
圆x2+y2-6x=0的圆心恰为y2=2px(p>0)的焦点,则p的值为( )
| A、4 | B、5 | C、6 | D、7 |