题目内容
设函数f（x）（x∈R）满足f（x+2）=f（x）+2．当0≤x＜2时，f（x）=1，则f（2014）=（ ）
| A、2013 | B、2014 |
| C、2015 | D、2016 |
考点：抽象函数及其应用,函数的值
专题：函数的性质及应用
分析：根据递推式f（x+2）=f（x）+2进行递推，结合当0≤x＜2时，f（x）=1，从而可求出所求．
解答：
解：因为f（x+2）=f（x）+2，所以f（2014）=f（2012）+2=f（2010）+4=…=f（0）+2014，
而当0≤x＜2时，f（x）=1，则f（2014）=1+2014=2015．
故选C．
而当0≤x＜2时，f（x）=1，则f（2014）=1+2014=2015．
故选C．
点评：本题主要考查了抽象函数及其应用，解题的关键是熟练运用递推式f（x+2）=f（x）+2，同时考查了分析问题的能力．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
等差数列
，-
，-
，-
，…的一个通项公式是（ ）
| 3 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| 9 |
| 2 |
A、2n-
| ||
B、
| ||
C、
| ||
D、
|
一元二次方程2x2-6x-3=0的两根为x1，x2，则（1+x1）（1+x2）的值为（ ）
| A、3 | ||
| B、6 | ||
| C、-3 | ||
D、
|
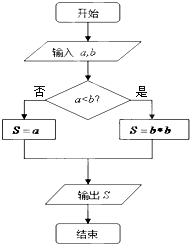对于给定的实数a、b，定义运算“⊕”：s=a⊕b．若其运算法则如程序框图所示，则集合{y|y=（1⊕x）•x+（2⊕x），x∈[-2，2]}（注：“•”和“+”表示实数的乘法和加法运算）的最大元素是已知集合A={0，1，2，3}，B={1，3，4}，则A∩B的子集个数为（ ）
| A、2 | B、3 | C、4 | D、16 |