题目内容
已知函数f(x)满足f(0)=2,且对任意实数x,f(x)-f′(x)>1恒成立,则f(x)>ex+1的解集为 .
考点:函数恒成立问题
专题:导数的综合应用,不等式的解法及应用
分析:设h(x)=e-x•f(x)-e-x-1,则不等式f(x)>ex+1的解集就是 h(x)>0 的解集.由此利用导数性质能求出不等式f(x)>ex+1的解集.
解答:
解:设h(x)=e-x•f(x)-e-x-1,
则不等式f(x)>ex+1同解于e-x•f(x)>e-x+1,
不等式f(x)>ex+1的解集就是 h(x)>0 的解集.
h(0)=1×2-1-1=0,
h′(x)=-e-x[f(x)-f′(x)]+e-x,
∵[f(x)-f′(x)]>1,
∴对于任意 x∈R,
e-x[f(x)-f′(x)]>e-x,
∴h′(x)=-e-x[f(x)-f′(x)]+ex<0.
即h(x)在实数域内单调递减.
∵h(0)=0,
∴当 x<0 时,f(x)>0;当 x>0 时,f(x)<0.
∴不等式f(x)>ex+1的解集为:{x|x<0}.
故答案为:(-∞,0).
则不等式f(x)>ex+1同解于e-x•f(x)>e-x+1,
不等式f(x)>ex+1的解集就是 h(x)>0 的解集.
h(0)=1×2-1-1=0,
h′(x)=-e-x[f(x)-f′(x)]+e-x,
∵[f(x)-f′(x)]>1,
∴对于任意 x∈R,
e-x[f(x)-f′(x)]>e-x,
∴h′(x)=-e-x[f(x)-f′(x)]+ex<0.
即h(x)在实数域内单调递减.
∵h(0)=0,
∴当 x<0 时,f(x)>0;当 x>0 时,f(x)<0.
∴不等式f(x)>ex+1的解集为:{x|x<0}.
故答案为:(-∞,0).
点评:本题考查不等式的解集的求法,是中档题,解题时要认真审题,注意导数性质的灵活运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
一元二次方程2x2-6x-3=0的两根为x1,x2,则(1+x1)(1+x2)的值为( )
| A、3 | ||
| B、6 | ||
| C、-3 | ||
D、
|
下列选项中,可作为函数y=f(x)的图象的是( )
A、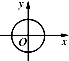 |
B、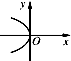 |
C、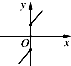 |
D、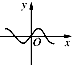 |
已知集合A={0,1,2,3},B={1,3,4},则A∩B的子集个数为( )
| A、2 | B、3 | C、4 | D、16 |
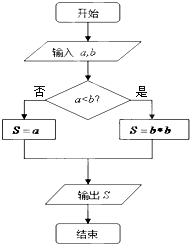 对于给定的实数a、b,定义运算“⊕”:s=a⊕b.若其运算法则如程序框图所示,则集合{y|y=(1⊕x)•x+(2⊕x),x∈[-2,2]}(注:“•”和“+”表示实数的乘法和加法运算)的最大元素是
对于给定的实数a、b,定义运算“⊕”:s=a⊕b.若其运算法则如程序框图所示,则集合{y|y=(1⊕x)•x+(2⊕x),x∈[-2,2]}(注:“•”和“+”表示实数的乘法和加法运算)的最大元素是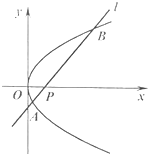 如图,已知抛物线y2=4x,点P(a,0)是x轴上的一点,经过点P且斜率为1的直线l与抛物线相交于A,B两点.
如图,已知抛物线y2=4x,点P(a,0)是x轴上的一点,经过点P且斜率为1的直线l与抛物线相交于A,B两点.