题目内容
已知直线l:
(t为参数),与曲线C:x2=y交于A、B两点,P(3,-1)是平面内的一个定点,则|PA|+|PB|= .
|
考点:直线的参数方程
专题:坐标系和参数方程
分析:把直线l的参数方程化为普通方程,与曲线C的方程组成方程组,求出A、B点的坐标,即可求出|PA|+|PB|的值.
解答:
解:直线l:
(t为参数)化为普通方程是
x+3y=0,
l与曲线C:x2=y交于A、B两点,
∴
;
消去y,得x+3x2=0,
解得x=0,或x=-
;
当x=0时,y=0;
当x=-
时,y=
;
∴A(0,0),B(-
,
);
∴|PA|+|PB|=
+
=
.
故答案为:
.
|
x+3y=0,
l与曲线C:x2=y交于A、B两点,
∴
|
消去y,得x+3x2=0,
解得x=0,或x=-
| 1 |
| 3 |
当x=0时,y=0;
当x=-
| 1 |
| 3 |
| 1 |
| 9 |
∴A(0,0),B(-
| 1 |
| 3 |
| 1 |
| 9 |
∴|PA|+|PB|=
| (3-0)2+(-1-0)2 |
(3+
|
19
| ||
| 9 |
故答案为:
19
| ||
| 9 |
点评:本题考查了参数方程的应用问题,解题时应先把参数方程化为普通方程,再进行解答,是基础题.

练习册系列答案
相关题目
在等差数列{an}中,a3+a5=10,a7=2,则a1=( )
| A、5 | B、8 | C、10 | D、14 |
下列说法错误的是( )
| A、命题“若a>-3,则a>-6”以及它的逆命题、否命题、逆否命题中,真命题的个数为2个 |
| B、对于命题p:?x∈R,使得x2+x+1<0;则?p:?x∈R,均有x2+x+1≥0 |
| C、命题“若m>0,则方程x2+x-m=0有实根”的逆否命题为“若方程x2+x-m=0无实根,则m≤0” |
| D、命题“若xy=0,则x、y中至少有一个为零”的否定是“若xy≠0,则x、y都不为零” |
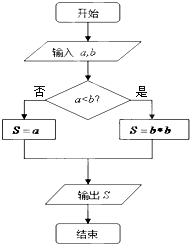 对于给定的实数a、b,定义运算“⊕”:s=a⊕b.若其运算法则如程序框图所示,则集合{y|y=(1⊕x)•x+(2⊕x),x∈[-2,2]}(注:“•”和“+”表示实数的乘法和加法运算)的最大元素是
对于给定的实数a、b,定义运算“⊕”:s=a⊕b.若其运算法则如程序框图所示,则集合{y|y=(1⊕x)•x+(2⊕x),x∈[-2,2]}(注:“•”和“+”表示实数的乘法和加法运算)的最大元素是