题目内容
若关于x的方程x2-2mx+m+6=0的两实根为x1,x2,y=(x1-1)2+(x2-1)2的取值范围是( )
A、y≥
| ||
| B、y≥8 | ||
| C、y≥18 | ||
D、y>-
|
考点:根与系数的关系
专题:函数的性质及应用
分析:由方程x2-2mx+m+6=0的两实根为x1,x2,可得:△≥0,即m≤-2,或m≥3,且x1+x2=2m,x1•x2=m+6,进而可将y=(x1-1)2+(x2-1)2化为:y=4m2-6m-10(m≤-2,或m≥3)的形式,结合二次函数的图象和性质可得答案.
解答:
解:∵方程x2-2mx+m+6=0的两实根为x1,x2,
∴△=4m2-4(m+6)≥0,即m≤-2,或m≥3,
且x1+x2=2m,x1•x2=m+6,
则y=(x1-1)2+(x2-1)2=(x1+x2)2-2x1•x2-2(x1+x2)+2=4m2-2(m+6)-4m+2=4m2-6m-10,
故当m=3时,y取最小值8,无最大值,
即y=(x1-1)2+(x2-1)2的取值范围是y≥8,
故选:B
∴△=4m2-4(m+6)≥0,即m≤-2,或m≥3,
且x1+x2=2m,x1•x2=m+6,
则y=(x1-1)2+(x2-1)2=(x1+x2)2-2x1•x2-2(x1+x2)+2=4m2-2(m+6)-4m+2=4m2-6m-10,
故当m=3时,y取最小值8,无最大值,
即y=(x1-1)2+(x2-1)2的取值范围是y≥8,
故选:B
点评:本题考查的知识点是一元二次方程根与系数的关系,二次函数的图象和性质,难度中档.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
等差数列
,-
,-
,-
,…的一个通项公式是( )
| 3 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| 9 |
| 2 |
A、2n-
| ||
B、
| ||
C、
| ||
D、
|
已知集合A={0,1,2,3},B={1,3,4},则A∩B的子集个数为( )
| A、2 | B、3 | C、4 | D、16 |
在△ABC中,内角A,B,C的对边分别是a,b,c,若a2-b2-c2=
bc,A=( )
| 3 |
| A、30° | B、60° |
| C、120° | D、150° |
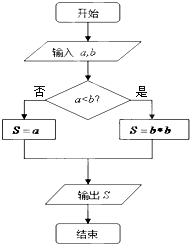 对于给定的实数a、b,定义运算“⊕”:s=a⊕b.若其运算法则如程序框图所示,则集合{y|y=(1⊕x)•x+(2⊕x),x∈[-2,2]}(注:“•”和“+”表示实数的乘法和加法运算)的最大元素是
对于给定的实数a、b,定义运算“⊕”:s=a⊕b.若其运算法则如程序框图所示,则集合{y|y=(1⊕x)•x+(2⊕x),x∈[-2,2]}(注:“•”和“+”表示实数的乘法和加法运算)的最大元素是