题目内容
2.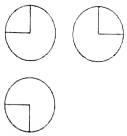 如图,某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径,半径长度为2,则该几何体的表面积是( )
如图,某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径,半径长度为2,则该几何体的表面积是( )| A. | 17π | B. | 18π | C. | 20π | D. | 28π |
分析 由三视图画出该几何体的直观图,分析可得该几何体是一个球被切掉左上角的八分之一,它的表面积是八分之七的球面面积和三个扇形面积之和,进而得到答案.
解答 解:由三视图知,该几何体的直观图如图所示:
该几何体是一个球被切掉左上角的八分之一,
即该几何体是八分之七个球,
球半径R=2,
所以它的表面积是八分之七的球面面积和三个扇形面积之和,
即$\frac{7}{8}$×4π×22+$\frac{3}{4}$×π×22=17π,
故选A.
点评 本题考查的知识点是球的体积和表面积,简单几何体的三视图,难度中档.

练习册系列答案
相关题目
13.函数f(x)=2sin(ωx+φ)(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,则ω,φ的值分别是( )

| A. | 2,-$\frac{π}{6}$ | B. | 2,-$\frac{π}{3}$ | C. | 4,-$\frac{π}{3}$ | D. | 4,-$\frac{π}{6}$ |
17.若函数y=f(x)在区间I上是增函数,且函数$y=\frac{f(x)}{x}$在区间I上是减函数,则称函数f(x)是区间I上的“H函数”.对于命题:①函数$f(x)=-x+2\sqrt{x}$是(0,1)上的“H函数”;②函数$g(x)=\frac{2x}{{1-{x^2}}}$是(0,1)上的“H函数”.下列判断正确的是( )
| A. | ①和②均为真命题 | B. | ①为真命题,②为假命题 | ||
| C. | ①为假命题,②为真命题 | D. | ①和②均为假命题 |
6.抛物线x2=$\frac{1}{4}$y上的一点M到焦点的距离为1,则点M到x轴的距离是( )
| A. | $\frac{17}{16}$ | B. | $\frac{15}{16}$ | C. | 1 | D. | $\frac{7}{8}$ |
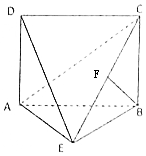 如图,四边形ABCD为矩形,DA⊥平面ABE,AE=EB=BC=2,BF⊥平面ACE于点F,且点F在CE上.
如图,四边形ABCD为矩形,DA⊥平面ABE,AE=EB=BC=2,BF⊥平面ACE于点F,且点F在CE上.