题目内容
10.已知向量$\overrightarrow a=(x,y)$(x,y∈R),$\overrightarrow b=(1,2)$,若x2+y2=1,则$|\overrightarrow a-\overrightarrow b|$的最大值为$\sqrt{5}$+1.分析 利用$|\overrightarrow a-\overrightarrow b|$≤$|\overrightarrow{OP}|$+r即可得出.
解答 解:设O(0,0),P(1,2).
$|\overrightarrow a-\overrightarrow b|$=$\sqrt{(x-1)^{2}+(y-2)^{2}}$≤$|\overrightarrow{OP}|$+r=$\sqrt{{1}^{2}+{2}^{2}}$+1=$\sqrt{5}$+1.
∴$|\overrightarrow a-\overrightarrow b|$的最大值为$\sqrt{5}$+1.
故答案为:$\sqrt{5}+1$.
点评 本题考查了向量的模的计算公式、点与圆的位置关系,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
20.用反证法证明命题“已知a、b、c为非零实数,且a+b+c>0,ab+bc+ca>0,求证a、b、c中至少有二个为正数”时,要做的假设是( )
| A. | a、b、c中至少有二个为负数 | B. | a、b、c中至多有一个为负数 | ||
| C. | a、b、c中至多有二个为正数 | D. | a、b、c中至多有二个为负数 |
15.关于直线l,m及平面α,β,下列命题中正确的是( )
| A. | 若l∥α,α∩β=m,则l∥m | B. | 若l∥α,m∥α,则l∥m | ||
| C. | 若l⊥α,m∥α,则l⊥m | D. | 若l∥α,m⊥l,则m⊥α |
2.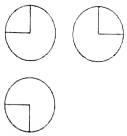 如图,某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径,半径长度为2,则该几何体的表面积是( )
如图,某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径,半径长度为2,则该几何体的表面积是( )
 如图,某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径,半径长度为2,则该几何体的表面积是( )
如图,某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径,半径长度为2,则该几何体的表面积是( )| A. | 17π | B. | 18π | C. | 20π | D. | 28π |