题目内容
17.若函数y=f(x)在区间I上是增函数,且函数$y=\frac{f(x)}{x}$在区间I上是减函数,则称函数f(x)是区间I上的“H函数”.对于命题:①函数$f(x)=-x+2\sqrt{x}$是(0,1)上的“H函数”;②函数$g(x)=\frac{2x}{{1-{x^2}}}$是(0,1)上的“H函数”.下列判断正确的是( )| A. | ①和②均为真命题 | B. | ①为真命题,②为假命题 | ||
| C. | ①为假命题,②为真命题 | D. | ①和②均为假命题 |
分析 对函数$f(x)=-x+2\sqrt{x}$,G(x)=$\frac{-x+2\sqrt{x}}{x}=\frac{2}{\sqrt{x}}-1$在(0,1)上的单调性进行判断,得命题①是真命题.对函数$g(x)=\frac{2x}{{1-{x^2}}}$=$\frac{2}{\frac{1}{x}-x}$,H(x)=$\frac{g(x)}{x}=\frac{1}{1-{x}^{2}}$在(0,1)上单调性进行判断,得命题②是假命题.
解答 解:对于命题①:令t=$\sqrt{x}$,函数$f(x)=-x+2\sqrt{x}$=-t2+2t,∵t=$\sqrt{x}$在(0,1)上是增函数,
函数y=-t2+2t在(0,1)上是增函数,∴在(0,1)上是增函数;
G(x)=$\frac{-x+2\sqrt{x}}{x}=\frac{2}{\sqrt{x}}-1$在(0,1)上是减函数,
∴函数$f(x)=-x+2\sqrt{x}$是(0,1)上的“H函数“,故命题①是真命题.
对于命题②,函数$g(x)=\frac{2x}{{1-{x^2}}}$=$\frac{2}{\frac{1}{x}-x}$是(0,1)上的增函数,H(x)=$\frac{g(x)}{x}=\frac{1}{1-{x}^{2}}$是(0,1)上的增函数,故命题②是假命题;
故选:B.
点评 本题考查了命题真假的判定,涉及到了函数的单调性,属于中档题.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
8.函数y=ax+1(a>0,a≠1)的图象必经过点( )
| A. | (0,1) | B. | (1,0) | C. | (0,2) | D. | (2,1) |
2.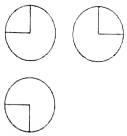 如图,某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径,半径长度为2,则该几何体的表面积是( )
如图,某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径,半径长度为2,则该几何体的表面积是( )
 如图,某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径,半径长度为2,则该几何体的表面积是( )
如图,某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径,半径长度为2,则该几何体的表面积是( )| A. | 17π | B. | 18π | C. | 20π | D. | 28π |
9.一个年级有12个班,每个班有50名学生,随机编号为1~50,为了了解他们课外的兴趣,要求每班第40号学生留下来进行问卷调查,这运用的抽样方法是( )
| A. | 分层抽样 | B. | 抽签法 | C. | 随机数表法 | D. | 系统抽样法 |
1.函数f(x)满足对于任意实数x,都有f(-x)=f(x),且当x1,x2∈[0,+∞),x1≠x2时,$\frac{{f({x_1})-f({x_2})}}{{{x_1}-x}}>0$都成立,则下列结论正确的是( )
| A. | f(-2)>f(0)>f(1) | B. | f(-2)>f(1)>f(0) | C. | f(1)>f(0)>f(-2) | D. | f(1)>f(-2)>f(0) |
 已知在长方体ABCD-A1B1C1D1中,E,M,N分别是BC,AE,D1C的中点,AD=AA1,AB=2AD.
已知在长方体ABCD-A1B1C1D1中,E,M,N分别是BC,AE,D1C的中点,AD=AA1,AB=2AD.