题目内容
13.函数f(x)=2sin(ωx+φ)(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,则ω,φ的值分别是( )
| A. | 2,-$\frac{π}{6}$ | B. | 2,-$\frac{π}{3}$ | C. | 4,-$\frac{π}{3}$ | D. | 4,-$\frac{π}{6}$ |
分析 根据图象的两个点A、B的横坐标,得到四分之三个周期的值,得到周期的值,做出ω的值,把图象所过的一个点的坐标代入方程做出初相,写出解析式,代入数值得到结果.
解答 解:由图象可得:$\frac{3T}{4}$=$\frac{5π}{12}$-(-$\frac{π}{3}$)=$\frac{3π}{4}$,
∴T=$\frac{2π}{ω}$=π,
∴ω=2,
又由函数f(x)的图象经过($\frac{5π}{12}$,2),
∴2=2sin(2×$\frac{5π}{12}$+φ),
∴$\frac{5π}{6}$+φ=2kπ+$\frac{π}{2}$,(k∈Z),
即φ=2kπ-$\frac{π}{3}$,k∈Z,
又由-$\frac{π}{2}$<φ<$\frac{π}{2}$,则φ=-$\frac{π}{3}$.
故选:B.
点评 本题考查有部分图象确定函数的解析式,本题解题的关键是确定初相的值,这里利用代入点的坐标求出初相,属于基础题.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案 培优三好生系列答案
培优三好生系列答案
相关题目
8.函数y=ax+1(a>0,a≠1)的图象必经过点( )
| A. | (0,1) | B. | (1,0) | C. | (0,2) | D. | (2,1) |
2.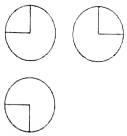 如图,某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径,半径长度为2,则该几何体的表面积是( )
如图,某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径,半径长度为2,则该几何体的表面积是( )
 如图,某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径,半径长度为2,则该几何体的表面积是( )
如图,某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径,半径长度为2,则该几何体的表面积是( )| A. | 17π | B. | 18π | C. | 20π | D. | 28π |
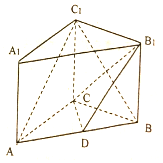 如图,已知在侧棱垂直于底面的三棱柱ABC-A1B1C1中,AC=3,AB=5,BC=4,AA1=4点D是AB的中点.
如图,已知在侧棱垂直于底面的三棱柱ABC-A1B1C1中,AC=3,AB=5,BC=4,AA1=4点D是AB的中点.