题目内容
已知焦点在x轴上的双曲线
-
=1实轴长为4,离心率等于
.
(1)写出双曲线方程;
(2)若该双曲线的左、右顶点分别为A1,A2,点P(x1,y1),Q(x1,-y1)是双曲线上不同的两个动点.求直线A1P与A2Q交点的轨迹E的方程.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
(1)写出双曲线方程;
(2)若该双曲线的左、右顶点分别为A1,A2,点P(x1,y1),Q(x1,-y1)是双曲线上不同的两个动点.求直线A1P与A2Q交点的轨迹E的方程.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线的定义、性质与方程
分析:(1)由已知得a,b,c的方程组,解之得a,b,c的值,方程可求;
(2)可采用交轨法,即先把A1P,A2Q的方程用已知点A1和A2、以及P、Q的坐标分别表示出来,两者联立,消去x1,y1后得到的关于x,y的方程即为交点的轨迹方程,注意轨迹方程中x,y的范围.
(2)可采用交轨法,即先把A1P,A2Q的方程用已知点A1和A2、以及P、Q的坐标分别表示出来,两者联立,消去x1,y1后得到的关于x,y的方程即为交点的轨迹方程,注意轨迹方程中x,y的范围.
解答:
解:(1)由已知得
,解得a=2,c=
,b=
,
所以方程为
-
=1;
(2)由A1、A2为双曲线的左、右顶点知,A1(-2,0),A2(2,0),又P(x1,y1),Q(x1,-y1)
所以A1P方程:y=
(x+2),A2Q方程:y=
(x-2),
两式相乘得y2=
(x2-4),
而点P(x1,y1)在双曲线上,
-
=1,
即-y12=3(1-
)
故y2=-
(x2-4)即
+
=1,
因为点P,Q是双曲线上的不同两点,所以它们与点A1,A2均不重合,故点A1和A2均不在轨迹E上,
过点(0,
)及A2(2,0)的直线l与双曲线只有唯一交点A2,故轨迹E不过点(0,
),同理轨迹E也不过点(0,-
).
综上分析,轨迹E的方程为
+
=1,(x≠0且x≠±2).
|
| 7 |
| 3 |
所以方程为
| x2 |
| 4 |
| y2 |
| 3 |
(2)由A1、A2为双曲线的左、右顶点知,A1(-2,0),A2(2,0),又P(x1,y1),Q(x1,-y1)
所以A1P方程:y=
| y1-0 |
| x1+2 |
| -y1-0 |
| x1-2 |
两式相乘得y2=
| -y12 |
| x12-4 |
而点P(x1,y1)在双曲线上,
| x12 |
| 4 |
| y12 |
| 3 |
即-y12=3(1-
| x12 |
| 4 |
故y2=-
| 3 |
| 4 |
| x2 |
| 4 |
| y2 |
| 3 |
因为点P,Q是双曲线上的不同两点,所以它们与点A1,A2均不重合,故点A1和A2均不在轨迹E上,
过点(0,
| 3 |
| 3 |
| 3 |
综上分析,轨迹E的方程为
| x2 |
| 4 |
| y2 |
| 3 |
点评:本题重点考查双曲线的标准方程的求法,以及利用交轨法求轨迹方程的问题,利用交轨法求轨迹方程的关键在于先求出产生交点的两曲线(或直线)的方程,然后两者联立,消去参数即可,要注意方程中x,y的取值范围.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
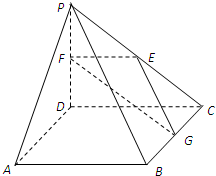 如图,在四棱锥P-ABCD中,ABCD是正方形,PD⊥平面ABCD,PD=AB=2,E,F,G分别是PC,PD,BC的中点.
如图,在四棱锥P-ABCD中,ABCD是正方形,PD⊥平面ABCD,PD=AB=2,E,F,G分别是PC,PD,BC的中点. 某校从参加高一年级期末考试的学生中抽出60名学生,将其成绩(均为整数)分成六段(即六组)[40,50),[50,60),…[90,100]后,画出如图部分频率分布直方图.请根据图形的信息,回答下列问题:
某校从参加高一年级期末考试的学生中抽出60名学生,将其成绩(均为整数)分成六段(即六组)[40,50),[50,60),…[90,100]后,画出如图部分频率分布直方图.请根据图形的信息,回答下列问题: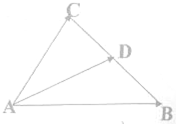 已知|
已知|