题目内容
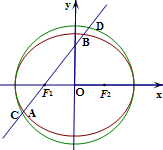 如图所示,椭圆Γ:
如图所示,椭圆Γ:| x2 |
| a2 |
| y2 |
| b2 |
(1)求椭圆Γ的方程;
(2)过左焦点F1的直线l与椭圆Γ相交于A,B两点,与圆x2+y2=a2相交于C,D两点,求
| |AB| |
| |CD| |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)设P是椭圆Γ上任意一点,则|PF1|-|PF2|≤|F1F2|=2c,故c=1.解方程4x2-8x+3=0,得
=e=
,由此能求出椭圆Γ的方程.
(2)法一:焦准距p=
-c=3,设∠OF1B=θ(0≤θ<π),由已知条件推导出
=
•
.令t=4-cos2θ∈[3,4],则
=
.令f(t)=t2(7-t),则f'(t)=-3t2+14t=t(14-3t)>0,由此求出
的最小值为
,取得最小值直线l的方程为x=-1.
(2)法二:当l⊥x轴时,|AB|=3,|CD|=2
,有
=
.当l与x轴不垂直时,设l:y=k(x+1),代入
+
=1,得(4k2+3)x2+8k2x+4k2-12=0,由已和条件推导出
=
=
.由此能求出
的最小值为
,取得最小值直线l的方程为x=-1.
| 1 |
| 2 |
| c |
| a |
(2)法一:焦准距p=
| a2 |
| c |
| |AB|2 |
| |CD|2 |
| 1 |
| 3+cos2θ |
| 36 |
| (4-cos2θ)2 |
| |AB|2 |
| |CD|2 |
| 36 |
| t2(7-t) |
| |AB| |
| |CD| |
| ||
| 2 |
(2)法二:当l⊥x轴时,|AB|=3,|CD|=2
| 3 |
| |AB| |
| |CD| |
| ||
| 2 |
| x2 |
| 4 |
| y2 |
| 3 |
| |AB|2 |
| |CD|2 |
| 36t3 |
| (4t-1)2(3t+1) |
| 36 | ||||||
(
|
| |AB| |
| |CD| |
| ||
| 2 |
解答:
解:(1)设P是椭圆Γ上任意一点,
则|PF1|-|PF2|≤|F1F2|=2c,故c=1.
解方程4x2-8x+3=0,得x=
或x=
.
因0<e<1,故
=e=
,因此a=2,从而b2=3.
所以椭圆Γ的方程为
+
=1.
(2)解法一:焦准距p=
-c=3,设∠OF1B=θ(0≤θ<π),
则|F1B|=
,|F1A|=
,故|AB|=
.
|CD|=2
=2
,
故
=
•
.
令t=4-cos2θ∈[3,4],则
=
.
令f(t)=t2(7-t),则f'(t)=-3t2+14t=t(14-3t)>0,
故f(t)在[3,4]单调递增,从而f(t)≤f(4)=48,
得
≥
=
⇒
≥
,
当且仅当t=4即θ=
时取等号.
所以
的最小值为
,取得最小值直线l的方程为x=-1.
(2)解法二:当l⊥x轴时,|AB|=3,|CD|=2
,有
=
.
当l与x轴不垂直时,设l:y=k(x+1),
代入
+
=1,并整理得(4k2+3)x2+8k2x+4k2-12=0,
故|AB|2=(1+k2)(x1-x2)2=(1+k2)[(
)2-4•
]=(
)2.
圆心O到l的距离d=
,
故|CD|2=4(4-
)=
,
令t=k2+1,则
=
=
.
令s=
,且f(s)=s3-5s2-8s+48,
则f'(s)=3s2-10s-8=(3s+2)(s-4).
因t≥1,故s∈(0,1],因此f'(s)<0,从而f(s)<f(0)=48,
>
=
⇒
>
.
综上知
的最小值为
,取得最小值直线l的方程为x=-1.
则|PF1|-|PF2|≤|F1F2|=2c,故c=1.
解方程4x2-8x+3=0,得x=
| 1 |
| 2 |
| 3 |
| 2 |
因0<e<1,故
| 1 |
| 2 |
| c |
| a |
所以椭圆Γ的方程为
| x2 |
| 4 |
| y2 |
| 3 |
(2)解法一:焦准距p=
| a2 |
| c |
则|F1B|=
| 3 |
| 2-cosθ |
| 3 |
| 2+cosθ |
| 12 |
| 4-cos2θ |
|CD|=2
| 22-sin2θ |
| 3+cos2θ |
故
| |AB|2 |
| |CD|2 |
| 1 |
| 3+cos2θ |
| 36 |
| (4-cos2θ)2 |
令t=4-cos2θ∈[3,4],则
| |AB|2 |
| |CD|2 |
| 36 |
| t2(7-t) |
令f(t)=t2(7-t),则f'(t)=-3t2+14t=t(14-3t)>0,
故f(t)在[3,4]单调递增,从而f(t)≤f(4)=48,
得
| |AB|2 |
| |CD|2 |
| 36 |
| 48 |
| 3 |
| 4 |
| |AB| |
| |CD| |
| ||
| 2 |
当且仅当t=4即θ=
| π |
| 2 |
所以
| |AB| |
| |CD| |
| ||
| 2 |
(2)解法二:当l⊥x轴时,|AB|=3,|CD|=2
| 3 |
| |AB| |
| |CD| |
| ||
| 2 |
当l与x轴不垂直时,设l:y=k(x+1),
代入
| x2 |
| 4 |
| y2 |
| 3 |
故|AB|2=(1+k2)(x1-x2)2=(1+k2)[(
| -8k2 |
| 4k2+3 |
| 4k2-12 |
| 4k2+3 |
| 12k2+12 |
| 4k2+3 |
圆心O到l的距离d=
| |k| | ||
|
故|CD|2=4(4-
| k2 |
| k2+1 |
| 12k2+16 |
| k2+1 |
令t=k2+1,则
| |AB|2 |
| |CD|2 |
| 36t3 |
| (4t-1)2(3t+1) |
| 36 | ||||||
(
|
令s=
| 1 |
| t |
则f'(s)=3s2-10s-8=(3s+2)(s-4).
因t≥1,故s∈(0,1],因此f'(s)<0,从而f(s)<f(0)=48,
| |AB|2 |
| |CD|2 |
| 36 |
| 48 |
| 3 |
| 4 |
| |AB| |
| |CD| |
| ||
| 2 |
综上知
| |AB| |
| |CD| |
| ||
| 2 |
点评:本题考查椭圆方程的求法,考查两线段比值的最小值的求法,解题时要认真审题,注意导数性质的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,已知平面四边形ABCP中,D为PA的中点,PA⊥AB,CD∥AB,且PA=CD=2AB=4.将此平面四边形ABCP沿CD折成直二面角P-DC-B,连接PA、PB,设PB中点为E.
如图,已知平面四边形ABCP中,D为PA的中点,PA⊥AB,CD∥AB,且PA=CD=2AB=4.将此平面四边形ABCP沿CD折成直二面角P-DC-B,连接PA、PB,设PB中点为E.