题目内容
已知a,b,c分别为△ABC三个内角A,B,C的对边,a2=b2+c2-bc.
(Ⅰ)求A;
(Ⅱ)若a=2,求bsinB+csinC的最大值.
(Ⅰ)求A;
(Ⅱ)若a=2,求bsinB+csinC的最大值.
考点:余弦定理
专题:解三角形
分析:(Ⅰ)△ABC中,由条件利用余弦定理求得cosA=
,可得A=
.
(Ⅱ)由条件利用正弦定理可得 bsinB+csinC=
(b2+c2),再由条件利用基本不等式求得
(b2+c2)≤2
,可得bsinB+csinC的最大值.
| 1 |
| 2 |
| π |
| 3 |
(Ⅱ)由条件利用正弦定理可得 bsinB+csinC=
| ||
| 4 |
| ||
| 4 |
| 3 |
解答:
解:(Ⅰ)△ABC中,∵a2=b2+c2-bc,∴cosA=
=
,∴A=
.
(Ⅱ)若a=2,则2r=
=
,∴bsinB+csinC=
(b2+c2).
∵b2+c2-4=bc≤
,∴b2+c2-≤8,∴
(b2+c2)≤2
,
即bsinB+csinC的最大值为2
.
| b2+c2-a2 |
| 2bc |
| 1 |
| 2 |
| π |
| 3 |
(Ⅱ)若a=2,则2r=
| a |
| sinA |
4
| ||
| 3 |
| ||
| 4 |
∵b2+c2-4=bc≤
| b2+c2 |
| 2 |
| ||
| 4 |
| 3 |
即bsinB+csinC的最大值为2
| 3 |
点评:本题主要考查正弦定理和余弦定理的应用,基本不等式,已知三角函数值求角的大小,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
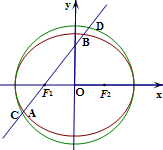 如图所示,椭圆Γ:
如图所示,椭圆Γ: 如图,已知A?α,B?α,PA,PB是平面α的两条斜线,且P?α,点P在α内的射影为O,若斜线PA、PB与平面α所成角相等.
如图,已知A?α,B?α,PA,PB是平面α的两条斜线,且P?α,点P在α内的射影为O,若斜线PA、PB与平面α所成角相等.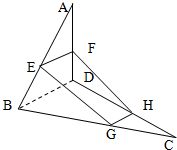 如图,空间四边形ABCD中,E,F分别是AB,AD边上的中点,G,H分别是BC,CD边上的点,且
如图,空间四边形ABCD中,E,F分别是AB,AD边上的中点,G,H分别是BC,CD边上的点,且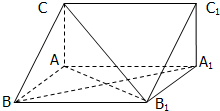 直三棱柱ABC-A1B1C1中,AB=AA1,∠CAB=
直三棱柱ABC-A1B1C1中,AB=AA1,∠CAB= 如图,AB是⊙O的一条切线,切点为B,ADE、CFD都是⊙O的割线,AC=AB,CE交⊙O于点G.
如图,AB是⊙O的一条切线,切点为B,ADE、CFD都是⊙O的割线,AC=AB,CE交⊙O于点G.