题目内容
已知两个不等的正整数x,y,满足
为质数,试比较x和y的大小关系.
| x2 |
| x+y |
考点:不等式比较大小
专题:不等式的解法及应用
分析:由题意,令设
=m,(m为质数),分赋值m,值讨论即可
| x2 |
| x+y |
解答:
解:因为
为质数,
设
=m,(m为质数)
则y=
-x,
令m=2时,
∴y=
-x
∵两个不等的正整数x,y
当x=2时,y=0不成立,当x=4时,y=4不成立,
当x=6时,y=12,当x=8时,y=24,
故y>x.
| x2 |
| x+y |
设
| x2 |
| x+y |
则y=
| x2 |
| m |
令m=2时,
∴y=
| x2 |
| 2 |
∵两个不等的正整数x,y
当x=2时,y=0不成立,当x=4时,y=4不成立,
当x=6时,y=12,当x=8时,y=24,
故y>x.
点评:本题主要考查了不等式的大小比较,采用赋值法,找到规律即可.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 有一海湾,海岸线近似为椭圆的一段弧NM,M、N为椭圆弧上两点,且MA⊥AB,NB⊥AB,AB间的距离为2公里,椭圆焦点为A、B,椭圆的短半轴长为
有一海湾,海岸线近似为椭圆的一段弧NM,M、N为椭圆弧上两点,且MA⊥AB,NB⊥AB,AB间的距离为2公里,椭圆焦点为A、B,椭圆的短半轴长为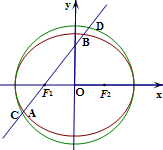 如图所示,椭圆Γ:
如图所示,椭圆Γ: 如图,已知A?α,B?α,PA,PB是平面α的两条斜线,且P?α,点P在α内的射影为O,若斜线PA、PB与平面α所成角相等.
如图,已知A?α,B?α,PA,PB是平面α的两条斜线,且P?α,点P在α内的射影为O,若斜线PA、PB与平面α所成角相等.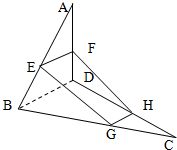 如图,空间四边形ABCD中,E,F分别是AB,AD边上的中点,G,H分别是BC,CD边上的点,且
如图,空间四边形ABCD中,E,F分别是AB,AD边上的中点,G,H分别是BC,CD边上的点,且