题目内容
判断函数y=
+x3的奇偶性并证明.
| 3 | x |
考点:函数奇偶性的判断
专题:函数的性质及应用
分析:根据奇偶性的定义,判断f(-x)与f(x)之间的关系,即可判断函数f(x)的奇偶性;
解答:
解:函数y=
+x3的定义域为R,
∵f(-x)=
+(-x)3=-
-x3=-f(x),
故函数y=
+x3为奇函数.
| 3 | x |
∵f(-x)=
| 3 | -x |
| 3 | x |
故函数y=
| 3 | x |
点评:此题主要考查函数的奇偶性,解题的关键是利用定义进行判断,是一道基础题.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
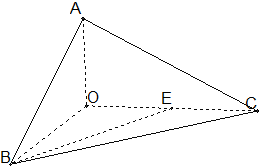 如图,已知三棱锥O-ABC的侧棱OA,OB,OC两两垂直,且OA=1,OB=OC=2,E是OC的中点.
如图,已知三棱锥O-ABC的侧棱OA,OB,OC两两垂直,且OA=1,OB=OC=2,E是OC的中点. 有一海湾,海岸线近似为椭圆的一段弧NM,M、N为椭圆弧上两点,且MA⊥AB,NB⊥AB,AB间的距离为2公里,椭圆焦点为A、B,椭圆的短半轴长为
有一海湾,海岸线近似为椭圆的一段弧NM,M、N为椭圆弧上两点,且MA⊥AB,NB⊥AB,AB间的距离为2公里,椭圆焦点为A、B,椭圆的短半轴长为 如图所示,在直四棱柱ABCD-A1B1C1D1中,底面ABCD是矩形,AB=1,BC=
如图所示,在直四棱柱ABCD-A1B1C1D1中,底面ABCD是矩形,AB=1,BC=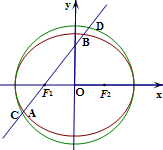 如图所示,椭圆Γ:
如图所示,椭圆Γ: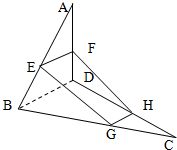 如图,空间四边形ABCD中,E,F分别是AB,AD边上的中点,G,H分别是BC,CD边上的点,且
如图,空间四边形ABCD中,E,F分别是AB,AD边上的中点,G,H分别是BC,CD边上的点,且