题目内容
已知数列{an}满足a1=x,a2=3x,Sn+1+Sn+Sn-1=3n2+2(n≥2,n∈N*),Sn是数列{an}的前n项和,若对?n∈N*,an<an+1恒成立,求实数x的取值范围.
考点:数列与不等式的综合
专题:等差数列与等比数列
分析:由已知条件推导出an+2+an+1+an=6n+3,n≥2,所以an+3+an+2+an+1=6(n+1)+3,作差,得an+3-an,n≥2,由此能求出实数x的取值范围.
解答:
解:由Sn+1+Sn+Sn-1=3n2+2,n≥2,n∈N*,
知Sn+2+Sn+1+Sn=3(n+1)2+2,n∈N*,
两式作差,得an+2+an+1+an=6n+3,n≥2,
∴an+3+an+2+an+1=6(n+1)+3,
作差,得an+3-an=6,n≥2,
∴n=1时,an=a1=x,
n=3k-1时,an=a3k-1=a2+(k-1)×6=2n+3x-4,
n=3k时,an=a3k=a3+(k-1)×6=2n-9x+8,
∵对任意n∈N*,an<an+1恒成立,
∴a1<a2,且a3k-1<a3k<a3k+1<a3k+2,
∴
,
解得
<x<
,
∴实数x的取值范围是(
,
).
知Sn+2+Sn+1+Sn=3(n+1)2+2,n∈N*,
两式作差,得an+2+an+1+an=6n+3,n≥2,
∴an+3+an+2+an+1=6(n+1)+3,
作差,得an+3-an=6,n≥2,
∴n=1时,an=a1=x,
n=3k-1时,an=a3k-1=a2+(k-1)×6=2n+3x-4,
n=3k时,an=a3k=a3+(k-1)×6=2n-9x+8,
∵对任意n∈N*,an<an+1恒成立,
∴a1<a2,且a3k-1<a3k<a3k+1<a3k+2,
∴
|
解得
| 13 |
| 15 |
| 7 |
| 6 |
∴实数x的取值范围是(
| 13 |
| 15 |
| 7 |
| 6 |
点评:本题考查实数的取值范围的求法,是中档题,解题时要认真审题,注意等价转化思想的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
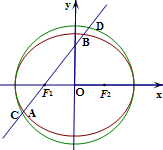 如图所示,椭圆Γ:
如图所示,椭圆Γ: 如图,已知A?α,B?α,PA,PB是平面α的两条斜线,且P?α,点P在α内的射影为O,若斜线PA、PB与平面α所成角相等.
如图,已知A?α,B?α,PA,PB是平面α的两条斜线,且P?α,点P在α内的射影为O,若斜线PA、PB与平面α所成角相等.