题目内容
用数学归纳法证明不等式:1+
+
+…+
>
时,第一步应验证n= 时,不等式成立.
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2n-1 |
| 127 |
| 64 |
考点:数学归纳法
专题:规律型,点列、递归数列与数学归纳法
分析:左边的和为
=2-21-n,再进行验证,即可得出结论.
1-
| ||
1-
|
解答:
解:左边的和为
=2-21-n,当n=8时,和为2-2-7>
,
故答案为:8.
1-
| ||
1-
|
| 127 |
| 64 |
故答案为:8.
点评:本题主要考查数学归纳法,起始值的验证,求解的关键是发现左边的规律,从而解决问题.

练习册系列答案
相关题目
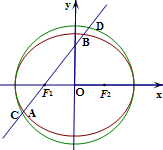 如图所示,椭圆Γ:
如图所示,椭圆Γ: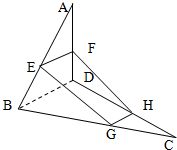 如图,空间四边形ABCD中,E,F分别是AB,AD边上的中点,G,H分别是BC,CD边上的点,且
如图,空间四边形ABCD中,E,F分别是AB,AD边上的中点,G,H分别是BC,CD边上的点,且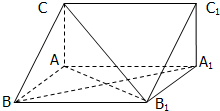 直三棱柱ABC-A1B1C1中,AB=AA1,∠CAB=
直三棱柱ABC-A1B1C1中,AB=AA1,∠CAB=
 如图,AB是⊙O的一条切线,切点为B,ADE、CFD都是⊙O的割线,AC=AB,CE交⊙O于点G.
如图,AB是⊙O的一条切线,切点为B,ADE、CFD都是⊙O的割线,AC=AB,CE交⊙O于点G.