题目内容
15．
如图，已知F1，F2是双曲线$C：\frac{x^2}{2}-\frac{y^2}{2}=1$的左，右焦点，点A在双曲线的右支上，线段AF1与双曲线左支相交于点B，△F2AB的内切圆与BF2相切于点E，若|AF2|=2|BF1|，则|BE|=$2\sqrt{2}$．
分析 设|BF1|=m，则|AF2|=2m，由双曲线的定义可得|AF1|=2a+2m，|BF2|=m+2a，|EF2|=m+2a-|BE|，再由内切圆的性质，求得a解得|BE|=2a=2$\sqrt{2}$．
解答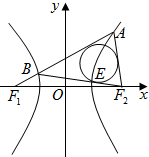 
解：设|BF1|=m，则|AF2|=2m，
由双曲线的定义有|AF1|=|AF2|+2a=2a+2m，
|BF2|=m+2a，|EF2|=m+2a-|BE|
∵|AB|=|AF2|-|EF2|+|BE|=2m-（m+2a-|BE|）+|BE|
∴|AF1|=∵|AB|+|BF1|
即有2a+2m=2m-（m+2a-|BE|）+|BE|+m，
解得|BE|=2a=2$\sqrt{2}$．
故答案为：2$\sqrt{2}$．
点评 本题考查双曲线的定义、方程和性质，考查内切圆的性质，考查定义法，属于中档题
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
5．函数f（x）=sinωx+$\sqrt{3}$cosωx+1的最小正周期为π，当x∈[m，n]时，f（x）至少有12个零点，则n-m的最小值为（ ）
| A． | 12π | B． | $\frac{7π}{3}$ | C． | 6π | D． | $\frac{16π}{3}$ |
3．在复平面内，复数$\frac{2-i}{1-i}$（i是虚数单位）对应的点在（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
10．设等差数列{an}的前n项和为Sn，若2a3=3+a1，则S9的值为（ ）
| A． | 15 | B． | 27 | C． | 30 | D． | 40 |
20．下列命题中正确的是（ ）
| A． | 若p∨q为真命题，则p∧q为真命题 | |
| B． | “x=5”是“x2-4x-5=0”的充分不必要条件 | |
| C． | 命题“若x＜-1，则x2-2x-3＞0”的否命题为：“若x＜-1，则x2-2x-3≤0” | |
| D． | 已知命题p：?x∈R，x2+x-1＜0，则￢p：?x∈R，x2+x-1≥0 |
7．一个几何体的三视图如图所示，则此几何体的体积为（ ）
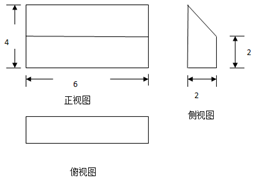
| A． | 16 | B． | 36 | C． | 48 | D． | 72 |
4．在四棱锥P-ABCD中，底面ABCD是正方形，PA⊥底面ABCD，PA=AB，E，F，H分别是棱PA，PB，AD的中点，且过E，F，H的平面截四棱锥P-ABCD所得截面面积为$\frac{{3\sqrt{2}}}{2}$，则四棱锥P-ABCD的体积为（ ）
| A． | $\frac{8}{3}$ | B． | 8 | C． | $8\sqrt{3}$ | D． | $24\sqrt{3}$ |