题目内容
5.已知定圆M:(x-3)2+y2=16和圆M所在平面内一定点A,点P是圆M上一动点,线段PA的垂直平分线l交直线PM于点Q.(Ⅰ)讨论Q点的轨迹可能是下面的情形中的哪几种:①椭圆;②双曲线;③抛物线;④圆;⑤直线;⑥一个点.
(Ⅱ)若定点A(5,0),试求△QMA的面积的最大值.
分析 (I)对A与圆M的位置关系进行讨论,利用圆锥曲线的定义得出结论;
(II)求出Q的轨迹所在椭圆的长短轴和焦距,得出三角形面积的最大值.
解答 解:(I)∵Q是线段PA的中垂线上的点,∴QA=PQ,
(1)若A在圆M外部,则|QA-QM|=|PQ-QM|=PM=4,MA>4,
∴Q点轨迹是以A,M为焦点的双曲线;
(2)若A在圆M上,则PA的中垂线恒过圆心M,
即Q的轨迹为点M;
(3)若A在圆M内部,则MA<4,QM+QA=QM+QP=4,
∴Q点轨迹是以M,A为焦点的椭圆;
(4)若A为圆M的圆心,即A与M重合时,Q为半径PM的中点,
∴Q点轨迹是以M为圆心,以2为半径的圆.
综上,Q点轨迹可能是①②④⑥四种情况.
(II)∵(5-3)2+02<16,∴A点在圆M内部,且不与圆心M(3,0)重合,
∴Q轨迹是以M,A为焦点的椭圆,
设此椭圆的长轴长为2a,短轴长为2b,焦距为2c,
MA=2c=2,QA+MM=PM=2a=4,
∴c=1,a=2,∴b=$\sqrt{3}$.
∴当Q为椭圆短轴端点时,△QMA的面积取得最大值,
△QMA面积最大值为$\frac{1}{2}×2c×b$=$\sqrt{3}$.
点评 本题考查了圆锥曲线的定义,性质,属于中档题.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
10.阅读如图的程序框图,运行相应的程序,则输出s的值为( )
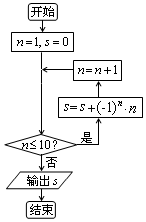

| A. | -6 | B. | 6 | C. | -5 | D. | 5 |
15.已知函数$f(x)=\left\{\begin{array}{l}1-{log_a}(x+2),x≥0\\ g(x),x<0\end{array}\right.$是奇函数,则方程g(x)=2的根为( )
| A. | $-\frac{3}{2}$ | B. | $\frac{3}{2}$ | C. | 6 | D. | -6 |
 如图,已知F1,F2是双曲线$C:\frac{x^2}{2}-\frac{y^2}{2}=1$的左,右焦点,点A在双曲线的右支上,线段AF1与双曲线左支相交于点B,△F2AB的内切圆与BF2相切于点E,若|AF2|=2|BF1|,则|BE|=$2\sqrt{2}$.
如图,已知F1,F2是双曲线$C:\frac{x^2}{2}-\frac{y^2}{2}=1$的左,右焦点,点A在双曲线的右支上,线段AF1与双曲线左支相交于点B,△F2AB的内切圆与BF2相切于点E,若|AF2|=2|BF1|,则|BE|=$2\sqrt{2}$.