题目内容
设函数fn(x)=xn(1-x)2在[
,1]上的最大值为an(n=1,2,…).
(1)求数列{an}的通项公式;
(2)证明:对任何正整数n(n≥2),都有an≤
成立;
(3)若数列{an}的前n之和为Sn,证明:对任意正整数n都有Sn<
成立.
| 1 |
| 2 |
(1)求数列{an}的通项公式;
(2)证明:对任何正整数n(n≥2),都有an≤
| 1 |
| (n+2)2 |
(3)若数列{an}的前n之和为Sn,证明:对任意正整数n都有Sn<
| 7 |
| 16 |
考点:数列的求和
专题:证明题,导数的综合应用,点列、递归数列与数学归纳法
分析:(1)易求f′n(x)=xn-1(1-x)[n(1-x)-2x],经分析可得n=1时,a1=f1(
)=
;当x∈[
,
)时f′n(x)>0,当x∈(
,1)时f′n(x)<0,函数fn(x)在x=
处取得最大值,从而可得数列{an}的通项公式;
(2)当n≥2时,利用分析法:要证an=
≤
,即证(1+
)n≥4,再利用二项式定理即可证得该式成立,从而使结论得证;
(3)当n=1,2时结论成立;当n≥3时,结合(2)的证明及放缩法的应用,即可证得对任意正整数n都有Sn<
成立.
| 1 |
| 2 |
| 1 |
| 8 |
| 1 |
| 2 |
| n |
| n+2 |
| n |
| n+2 |
| n |
| n+2 |
(2)当n≥2时,利用分析法:要证an=
| 4nn |
| (n+2)n+2 |
| 1 |
| (n+2)2 |
| 2 |
| n |
(3)当n=1,2时结论成立;当n≥3时,结合(2)的证明及放缩法的应用,即可证得对任意正整数n都有Sn<
| 7 |
| 16 |
解答:
解:(1)由f′n(x)=nxn-1(1-x)2-2xn(1-x)=xn-1(1-x)[n(1-x)-2x],
当x∈[
,1]时,由f′(x)=0得x=1或x=
;
当n=1时,
=
∉[
,1],f′1(x)=0,则 a1=f1(
)=
;
当n=2时,
∈[
,1],则a2=f2(
)=
;
当n≥3时,
∈[
,1],
而当x∈[
,
)时f′n(x)>0,当x∈(
,1)时f′n(x)<0,
故函数fn(x)在x=
处取得最大值,
即:an=fn(
)=
,
综上:an=
…(6分)
(2)当n≥2时,要证an=
≤
,即证(1+
)n≥4,
而(1+
)n=
+
•(
)1+
•(
)2+…≥1+2+
•
≥4,
故不等式成立…(10分)
(3)当n=1,2时结论成立;
当n≥3时,由(2)的证明可知:Sn=
+
+a3+a4+…+an<
+
+
+
+…+
<
+
+(
-
)+(
-
)+…+(
-
)<
+
+
=
,
从而Sn<
…(13分)
当x∈[
| 1 |
| 2 |
| n |
| n+2 |
当n=1时,
| n |
| n+2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 8 |
当n=2时,
| n |
| n+2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 16 |
当n≥3时,
| n |
| n+2 |
| 1 |
| 2 |
而当x∈[
| 1 |
| 2 |
| n |
| n+2 |
| n |
| n+2 |
故函数fn(x)在x=
| n |
| n+2 |
即:an=fn(
| n |
| n+2 |
| 4nn |
| (n+2)n+2 |
综上:an=
|
(2)当n≥2时,要证an=
| 4nn |
| (n+2)n+2 |
| 1 |
| (n+2)2 |
| 2 |
| n |
而(1+
| 2 |
| n |
| C | 0 n |
| C | 1 n |
| 2 |
| n |
| C | 2 n |
| 2 |
| n |
| n(n-1) |
| 2 |
| 4 |
| n2 |
故不等式成立…(10分)
(3)当n=1,2时结论成立;
当n≥3时,由(2)的证明可知:Sn=
| 1 |
| 8 |
| 1 |
| 16 |
| 1 |
| 8 |
| 1 |
| 16 |
| 1 |
| 52 |
| 1 |
| 62 |
| 1 |
| (n+2)2 |
| 1 |
| 8 |
| 1 |
| 16 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 5 |
| 1 |
| 6 |
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| 8 |
| 1 |
| 16 |
| 1 |
| 4 |
| 7 |
| 16 |
从而Sn<
| 7 |
| 16 |
点评:本题考查数列的求和,考查数列通项公式的确定,突出考查导数的应用,考查分析法、放缩法的综合应用及推理论证能力,属于难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
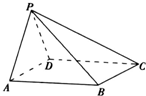 如图,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面PDC.
如图,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面PDC.