题目内容
已知函数f(x)=x|x-2a|-2x,x∈R.
(1)当a=
时,函数y=f(x)-m有三个零点,求实数m的取值范围;
(2)讨论函数y=f(x)的单调性.
(1)当a=
| 1 |
| 2 |
(2)讨论函数y=f(x)的单调性.
考点:函数零点的判定定理
专题:函数的性质及应用
分析:(1)需要分类讨论,当x≥1时,f(x)=x2-3x,当x<1时,f(x)=-x2+x,再根据方程的根的个数判断函数y=f(x)-m零点的情况.
(2需要分类讨论,当x≥2a时,当x<2a时,再求二次函数的单调区间.
(2需要分类讨论,当x≥2a时,当x<2a时,再求二次函数的单调区间.
解答:
解:(1)∵f(x)=x|x-2a|-2x,a=
,
∴f(x)=x|x-1|-2x
当x≥1时,f(x)=x2-3x,
当x<1时,f(x)=-x2+x
函数y=f(x)-m有三个零点,
∴f(x)-m=0有三个实数根.
①x≥1时,x2-3x-m=0,△=9+4m,
当9+4m>0时,即m>-
方程有两个不相等的实数根,
当9+4m=0,即m=-
方程有两个相等的实数根,
②x<1时,-x2+x-m=0,即,x2-x+m=0,△=1-4m,
当1-4m>0时,即m>
方程有两个不相等的实数根,
当1-4m=0,即m=
方程有两个相等的实数根,
综上所述,当m=
时,函数y=f(x)-m有三个零点
(2)①当x≥2a时,f(x)=x2-2(a+1)x=[x-(a+1)]2-(a+1)2,
x∈(-∞,a+1)时,f(x)为单调减函数,
x∈[a+1,2a]时,f(x)为单调增函数,
②当x<2a时,f(x)=-x2+2(a-1)x=-[x-(a-1)]2+(a-1)2,
x∈[a-1,2a)时,f(x)为单调减函数,
x∈(-∞,a-1)时,f(x)为单调增函数,
| 1 |
| 2 |
∴f(x)=x|x-1|-2x
当x≥1时,f(x)=x2-3x,
当x<1时,f(x)=-x2+x
函数y=f(x)-m有三个零点,
∴f(x)-m=0有三个实数根.
①x≥1时,x2-3x-m=0,△=9+4m,
当9+4m>0时,即m>-
| 9 |
| 4 |
当9+4m=0,即m=-
| 9 |
| 4 |
②x<1时,-x2+x-m=0,即,x2-x+m=0,△=1-4m,
当1-4m>0时,即m>
| 1 |
| 4 |
当1-4m=0,即m=
| 1 |
| 4 |
综上所述,当m=
| 1 |
| 4 |
(2)①当x≥2a时,f(x)=x2-2(a+1)x=[x-(a+1)]2-(a+1)2,
x∈(-∞,a+1)时,f(x)为单调减函数,
x∈[a+1,2a]时,f(x)为单调增函数,
②当x<2a时,f(x)=-x2+2(a-1)x=-[x-(a-1)]2+(a-1)2,
x∈[a-1,2a)时,f(x)为单调减函数,
x∈(-∞,a-1)时,f(x)为单调增函数,
点评:本题主要考查了函数零点的问题和函数的单调性的问题,属于中档题.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
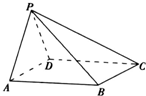 如图,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面PDC.
如图,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面PDC.
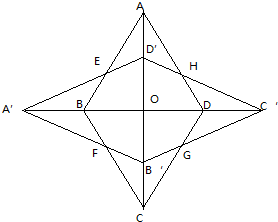 如图,菱形ABCD的对角线AC、BD相交于点O,AO=2BO=4,将菱形ABCD逆时针旋转90°得到菱形A′B′C′D′,求两个菱形重合部分的面积.
如图,菱形ABCD的对角线AC、BD相交于点O,AO=2BO=4,将菱形ABCD逆时针旋转90°得到菱形A′B′C′D′,求两个菱形重合部分的面积.