题目内容
已知函数f(x)=
x2+
x,数列{an}的前n项和为Sn,点(n,Sn)(n∈N*)均在函数y=f(x)的图象上.
(Ⅰ) 求数列{an}的通项公式an;
(Ⅱ)若bn=
,求数列{bn}的前n项和Tn.
| 1 |
| 2 |
| 1 |
| 2 |
(Ⅰ) 求数列{an}的通项公式an;
(Ⅱ)若bn=
| an |
| 2n |
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(Ⅰ)依题意可得2Sn=n2+n,n=1时a1=1;n≥2时可求得an=Sn-Sn-1=n,验证n=1符合后即可求得数列{an}的通项公式an;
(Ⅱ)Tn=
+2×(
)2+…+(n-1)•(
)n-1+n•(
)n,
Tn=(
)2+2×(
)3+…+(n-1)•(
)n+n•(
)n+1;利用错位相减法及等比数列的求和公式即可求得数列{bn}的前n项和Tn.
(Ⅱ)Tn=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:(I)∵点(n,Sn)(n∈N*)在函数y=f(x)的图象上,
∴Sn=
n2+
n,即2Sn=n2+n,①
n=1时a1=1;
n≥2时2Sn-1=(n-1)2+(n-1),②
故2(Sn-Sn-1)=2n,即an=n.
经验证n=1符合上式,故an=n.
(II)∵bn=n(
)n,
∴Tn=
+2×(
)2+…+(n-1)•(
)n-1+n•(
)n,
∴
Tn=(
)2+2×(
)3+…+(n-1)•(
)n+n•(
)n+1;
∴
Tn=
+(
)2+(
)3+…+(
)n-n•(
)n+1=
-n•(
)n+1=1-(
)n-n•(
)n+1,
∴Tn=2-(n+2)(
)n.
∴Sn=
| 1 |
| 2 |
| 1 |
| 2 |
n=1时a1=1;
n≥2时2Sn-1=(n-1)2+(n-1),②
故2(Sn-Sn-1)=2n,即an=n.
经验证n=1符合上式,故an=n.
(II)∵bn=n(
| 1 |
| 2 |
∴Tn=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||||
1-
|
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴Tn=2-(n+2)(
| 1 |
| 2 |
点评:本题考查数列的求和,着重考查等差数列通项公式的确定与错位相减法求数列的和,属于中档题.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
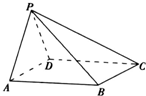 如图,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面PDC.
如图,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面PDC.