题目内容
15.sin$\frac{3π}{4}$=( )| A. | -$\frac{\sqrt{2}}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
分析 利用诱导公式,特殊角的三角函数值即可计算得解.
解答 解:sin$\frac{3π}{4}$=sin(π-$\frac{π}{4}$)=sin$\frac{π}{4}$=$\frac{\sqrt{2}}{2}$.
故选:D.
点评 本题主要考查了诱导公式,特殊角的三角函数值在三角函数化简求值中的应用,考查了转化思想,属于基础题.

练习册系列答案
相关题目
4.已知向量$\overrightarrow a=(x,-1)$,$\overrightarrow b=(1,\sqrt{3})$,若$\overrightarrow a⊥\overrightarrow b$,则$|\overrightarrow a|$=( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 4 |
3.已知命题:?x∈R,x2-ax+2a>0在R上恒成立,则实数a的取值范围是( )
| A. | (0,4) | B. | (-8,8) | C. | R | D. | (0,8) |
7.已知P(B|A)=$\frac{3}{10}$,P(A)=$\frac{1}{5}$,P(B)=$\frac{2}{3}$,则P(AB)=( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{5}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{50}$ |
4.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\;(a>0,b>0)$与函数$y=\sqrt{x}(x≥0)$的图象交于点P,若函数$y=\sqrt{x}$在点P处的切线过双曲线左焦点F(-1,0),则双曲线的离心率是( )
| A. | $\frac{{\sqrt{5}+1}}{2}$ | B. | $\frac{{\sqrt{5}+3}}{2}$ | C. | $\frac{{\sqrt{3}+1}}{2}$ | D. | $\frac{3}{2}$ |
5.已知函数f(x)=asinx+cosx(a为常数,x∈R)的图象关于直线$x=\frac{π}{6}$对称,则函数g(x)=sinx+acosx的图象( )
| A. | 关于点$({\frac{π}{3},0})$对称 | B. | 关于点$({\frac{2π}{3},0})$对称 | ||
| C. | 关于直线$x=\frac{π}{3}$对称 | D. | 关于直线$x=\frac{π}{6}$对称 |
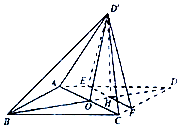 如图,菱形ABCD的对角线AC与BD交于点O,点E、F分别在AD,CD上,AE=EF,EF交BD于点H,将△DEF沿EF折到△D'EF的位置.
如图,菱形ABCD的对角线AC与BD交于点O,点E、F分别在AD,CD上,AE=EF,EF交BD于点H,将△DEF沿EF折到△D'EF的位置.