题目内容
4.已知向量$\overrightarrow a=(x,-1)$,$\overrightarrow b=(1,\sqrt{3})$,若$\overrightarrow a⊥\overrightarrow b$,则$|\overrightarrow a|$=( )| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 4 |
分析 根据题意,由$\overrightarrow a⊥\overrightarrow b$,则有$\overrightarrow{a}$•$\overrightarrow{b}$=x-$\sqrt{3}$=0,解可得x的值,即可得向量$\overrightarrow{a}$的坐标,由向量模的计算公式计算可得答案.
解答 解:根据题意,向量$\overrightarrow a=(x,-1)$,$\overrightarrow b=(1,\sqrt{3})$,
若$\overrightarrow a⊥\overrightarrow b$,则有$\overrightarrow{a}$•$\overrightarrow{b}$=x-$\sqrt{3}$=0,
解可得x=$\sqrt{3}$,
则$\overrightarrow{a}$=($\sqrt{3}$,-1),故$|\overrightarrow a|$=$\sqrt{3+1}$=2;
故选:C.
点评 本题考查向量的坐标运算,关键是掌握向量垂直与向量的数量积之间的关系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.已知x,y满足约束条件$\left\{\begin{array}{l}{x≥1}\\{y≥0}\\{x+y≤4}\end{array}\right.$则z=2x+3y的最大值为( )
| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
19.使函数f(x)=$\root{3}{{x}^{2}(1-{x}^{2})}$满足罗尔定理条件的区间是( )
| A. | [0,1] | B. | [-1,1] | C. | [-2,2] | D. | [-$\frac{3}{5}$,$\frac{4}{5}$] |
9.已知函数f(x)=(x2-3)ex,设关于x的方程${f^2}(x)-mf(x)-\frac{12}{e^2}=0(m∈R)$有n个不同的实数解,则n的所有可能的值为( )
| A. | 3 | B. | 1或3 | C. | 4或6 | D. | 3或4或6 |
15.sin$\frac{3π}{4}$=( )
| A. | -$\frac{\sqrt{2}}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
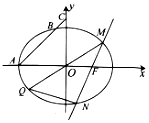 已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左顶点为A,右焦点为F(1,0),过点A且斜率为1的直线交椭圆E于另一点B,交y轴于点C,$\overrightarrow{AB}=6\overrightarrow{BC}$.
已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左顶点为A,右焦点为F(1,0),过点A且斜率为1的直线交椭圆E于另一点B,交y轴于点C,$\overrightarrow{AB}=6\overrightarrow{BC}$.