题目内容
7．已知P（B|A）=$\frac{3}{10}$，P（A）=$\frac{1}{5}$，P（B）=$\frac{2}{3}$，则P（AB）=（ ）| A． | $\frac{1}{2}$ | B． | $\frac{1}{5}$ | C． | $\frac{2}{3}$ | D． | $\frac{3}{50}$ |
分析 由条件概率的计算公式，可得P（AB）=P（A）×P（B|A），即可得出结论．
解答 解：由条件概率的计算公式，可得P（AB）=P（A）×P（B|A）=$\frac{1}{5}×\frac{3}{10}$=$\frac{3}{50}$，
故选D．
点评 本题考查条件概率，考查学生的计算能力，比较基础．
练习册系列答案
相关题目
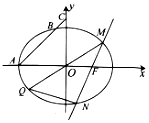已知椭圆E：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的左顶点为A，右焦点为F（1，0），过点A且斜率为1的直线交椭圆E于另一点B，交y轴于点C，$\overrightarrow{AB}=6\overrightarrow{BC}$．
15．sin$\frac{3π}{4}$=（ ）
| A． | -$\frac{\sqrt{2}}{2}$ | B． | -$\frac{1}{2}$ | C． | $\frac{1}{2}$ | D． | $\frac{\sqrt{2}}{2}$ |
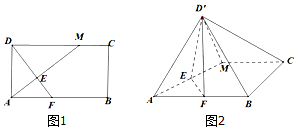如图，在矩形ABCD中，AB=2BC，点M在边CD上，点F在边AB上，且DF⊥AM，垂足为E，若将△ADM沿AM折起，使点D位于D′位置，连接D′B，D′C，得四棱锥D′-ABCM．