题目内容

3．已知命题：?x∈R，x2-ax+2a＞0在R上恒成立，则实数a的取值范围是（　　）
A．（0，4）B．（-8，8）C．RD．（0，8）

分析 将关于x的不等式x2-ax+2a＞0在R上恒成立，转化成△＜0，从而得到关于a的不等式，求得a的范围．

解答 解：因为不等式x2-ax+2a＞0在R上恒成立．
∴△=（-a）2-8a＜0，解得0＜a＜8
则实数a的取值范围是：（0，8）．
故选：D．

点评 本题主要考查了一元二次不等式的应用，以及恒成立问题的转化，同时考查了计算能力，属于基础题．

练习册系列答案
相关题目
11．已知函数f（x）=ex-ax．
（I ）若曲线y=f（x）在点（1，f（1））处的切线与直线y=ax+2平行．求实数a的值；
（Ⅱ）讨论f（x）的单调性；
（Ⅲ）当0＜a＜l时，证明：曲线y=f（x）在直线y=（e-1）x的上方．
12．在△ABC中，角A，B，C所对的边分别为a，b，c，已知a=2，c=5，$cosB=\frac{3}{5}$．则△ABC的面积为4．
9．已知函数f（x）=（x2-3）ex，设关于x的方程${f^2}（x）-mf（x）-\frac{12}{e^2}=0（m∈R）$有n个不同的实数解，则n的所有可能的值为（　　）
A．3B．1或3C．4或6D．3或4或6
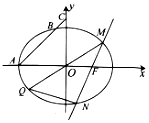16．已知椭圆E：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的左顶点为A，右焦点为F（1，0），过点A且斜率为1的直线交椭圆E于另一点B，交y轴于点C，$\overrightarrow{AB}=6\overrightarrow{BC}$．
（1）求椭圆E的方程；
（2）过点F作直线l与椭圆E交于M，N两点，连接MO（O为坐标原点）并延长交椭圆E于点Q，求△MNQ面积的最大值及取最大值时直线l的方程．
8．若双曲线x2-y2=2右支上一点（s，t）到直线y=x的距离为2，则s-t的值等于（　　）
A．2B．$2\sqrt{2}$C．-2D．$-2\sqrt{2}$
15．sin$\frac{3π}{4}$=（　　）
A．-$\frac{\sqrt{2}}{2}$B．-$\frac{1}{2}$C．$\frac{1}{2}$D．$\frac{\sqrt{2}}{2}$
12．数列{an}各项均为正数，且对任意n∈N*，满足an+1=an+can2（c＞0且为常数）．
（Ⅰ）若a1，2a2，3a3依次成等比数列，求a1的值（用常数c表示）；
（Ⅱ）设bn=$\frac{1}{1+c{a}_{n}}$，Sn是数列{bn}的前n项和，
（i）求证：$\frac{1}{{{a_{n+1}}}}-\frac{1}{a_n}=-\frac{c}{{1+c{a_n}}}$； 
（ii）求证：Sn＜Sn+1＜$\frac{1}{c{a}_{1}}$．
13．已知定义域为R的奇函数$f（x）=\frac{{-{2^x}+b}}{{{2^{x+1}}+2}}$．
（1）求b的值；
（2）证明函数f（x）为定义域上的单调递减函数；
（3）若对任意的t∈R，不等式f（t2-2t）+f（2t2-k）＜0恒成立，求k的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网