题目内容
 已知函数f(x)是定义域为R的偶函数,当x≥0时,f(x)=x(2-x).
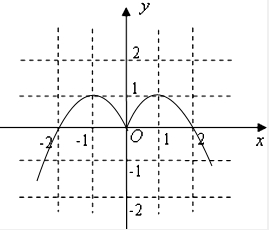
已知函数f(x)是定义域为R的偶函数,当x≥0时,f(x)=x(2-x).(1)在给定的图示中画出函数f(x)的图象(不需列表);
(2)求函数f(x)的解析式;
(3)讨论方程f(x)-k=0的根的情况.(只需写出结果,不要解答过程)
考点:函数奇偶性的性质,函数的图象
专题:函数的性质及应用
分析:(1)根据题意先画出f(x)在[0,+∞)上的图象,然后根据该函数为偶函数画出另一半的图象;
(2)根据偶函数的性质可以求出x<0时的解析式,然后得到整个定义域上的函数解析式;
(3)结合图象,利用数形结合的思想可获解.
(2)根据偶函数的性质可以求出x<0时的解析式,然后得到整个定义域上的函数解析式;
(3)结合图象,利用数形结合的思想可获解.
解答:
解:(1)由已知得函数f(x)的图象如图所示.
(2)设x≤0,则-x≥0,
∵当x≥0时,f(x)=x(2-x)
∴f(-x)=-x(x+2);
由f(x)是定义域为R的偶函数知:f(-x)=f(x),
∴f(x)=-x(x+2),(x∈(-∞,0]);…(3分)
所以函数f(x)的解析式是f(x)=
.
(3)由题意得:k=f(x),当k<0或k=1时,方程f(x)-k=0有两个根,
当k=0时,方程f(x)-k=0有三个根,
当0<k<1时,方程f(x)-k=0有四个根.
当k>1时,方程f(x)-k=0没有实数根.

(2)设x≤0,则-x≥0,
∵当x≥0时,f(x)=x(2-x)
∴f(-x)=-x(x+2);
由f(x)是定义域为R的偶函数知:f(-x)=f(x),
∴f(x)=-x(x+2),(x∈(-∞,0]);…(3分)
所以函数f(x)的解析式是f(x)=
|
(3)由题意得:k=f(x),当k<0或k=1时,方程f(x)-k=0有两个根,
当k=0时,方程f(x)-k=0有三个根,
当0<k<1时,方程f(x)-k=0有四个根.
当k>1时,方程f(x)-k=0没有实数根.
点评:本题考查了函数的偶函数的图象性质,以及利用图象解决方程的根的个数的问题,体现了数形结合思想的应用.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
已知{an}是等差数列,a7=12,则该数列前13项和S13等于( )
| A、156 | B、132 |
| C、110 | D、100 |
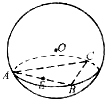 已知正△ABC三个顶点都在半径为2的球面上,球心O到平面ABC的距离为1,点E是线段AB的中点,过点E作球O的截面,则截面面积的最小值是( )
已知正△ABC三个顶点都在半径为2的球面上,球心O到平面ABC的距离为1,点E是线段AB的中点,过点E作球O的截面,则截面面积的最小值是( )A、
| ||
| B、2π | ||
C、
| ||
| D、3π |
 某空间几何体的三视图如图所示(单位:cm),则该几何体的体积V=
某空间几何体的三视图如图所示(单位:cm),则该几何体的体积V=