题目内容
已知A，B是单位圆C上的两个定点，对任意实数λ，|
-λ
|有最小值
，则|
|= ．
| AC |
| AB |
| 1 |
| 2 |
| AB |
考点：平面向量数量积的运算
专题：计算题,平面向量及应用
分析：由A，B是单位圆C上的两个定点，则|
|=|
|=1，令|
|=t，运用向量的平方即为模的平方，化简整理，结合余弦定理，可得关于λ的二次函数λ2t2-λt2+1，运用二次函数的最值，即可得到最小值，解方程进而得到t．
| AC |
| BC |
| AB |
解答：
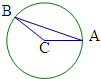解：由A，B是单位圆C上的两个定点，
则|
|=|
|=1，令|
|=t，
y=|
-λ
|2=（
-λ
）2=
2-2λ
•
+λ2|
|2
=1-2λ|
|•|
|cosA+λ2|
|2
=1-λ（t2+1-1）+λ2t2=λ2t2-λt2+1，
当λ=-
=
时，y取得最小值，且为
t2-
t2+1=1-
t2，
由于对任意实数λ，|
-λ
|有最小值
，
则1-
t2=
，解得t=
．
故答案为：
．
解：由A，B是单位圆C上的两个定点，则|
| AC |
| BC |
| AB |
y=|
| AC |
| AB |
| AC |
| AB |
| AC |
| AB |
| AC |
| AB |
=1-2λ|
| AB |
| AC |
| AB |
=1-λ（t2+1-1）+λ2t2=λ2t2-λt2+1，
当λ=-
| -t2 |
| 2t2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
由于对任意实数λ，|
| AC |
| AB |
| 1 |
| 2 |
则1-
| 1 |
| 4 |
| 1 |
| 4 |
| 3 |
故答案为：
| 3 |
点评：本题考查向量的数量积的定义和性质，主要考查向量的平方即为模的平方，运用二次函数的最值是解题的关键，属于中档题和易错题．
练习册系列答案
名校通行证有效作业系列答案
相关题目
某空间几何体的三视图如图所示（单位：cm），则该几何体的体积V=双曲线C：
-y2=1的两条渐近线夹角（锐角）为θ，则tanθ=（ ）
| x2 |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
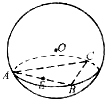已知正△ABC三个顶点都在半径为2的球面上，球心O到平面ABC的距离为1，点E是线段AB的中点，过点E作球O的截面，则截面面积的最小值是（ ）A、
| ||
| B、2π | ||
C、
| ||
| D、3π |
函数y=（2a2-3a+2）ax是指数函数，则a的取值范围是（ ）
| A、a＞0，a≠1 | ||
| B、0＜a＜1 | ||
C、a=
| ||
D、
|