题目内容
在△ABC中,角A,B,C的对边分别为a,b,c,且b2+a2=c2+
ab,则内角C=( )
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:余弦定理
专题:解三角形
分析:利用余弦定理表示出cosC,把已知等式变形后代入计算求出cosC的值,即可确定出C的度数.
解答:
解:∵在△ABC中,b2+a2=c2+
ab,即b2+a2-c2=
ab,
∴cosC=
=
,
则C=
,
故选:B.
| 2 |
| 2 |
∴cosC=
| a2+b2-c2 |
| 2ab |
| ||
| 2 |
则C=
| π |
| 4 |
故选:B.
点评:此题考查了余弦定理,以及特殊角的三角函数值,熟练掌握余弦定理是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知{an}是等差数列,a7=12,则该数列前13项和S13等于( )
| A、156 | B、132 |
| C、110 | D、100 |
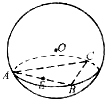 已知正△ABC三个顶点都在半径为2的球面上,球心O到平面ABC的距离为1,点E是线段AB的中点,过点E作球O的截面,则截面面积的最小值是( )
已知正△ABC三个顶点都在半径为2的球面上,球心O到平面ABC的距离为1,点E是线段AB的中点,过点E作球O的截面,则截面面积的最小值是( )A、
| ||
| B、2π | ||
C、
| ||
| D、3π |