题目内容
10.命题p:?x<0,x2≥2x,则命题¬p为( )| A. | ?x0<0,x${\;}_{0}^{2}$≥2${\;}^{{x}_{0}}$ | B. | ?x0≥0,x${\;}_{0}^{2}$≥2${\;}^{{x}_{0}}$ | ||
| C. | ?x0<0,x${\;}_{0}^{2}$<2${\;}^{{x}_{0}}$ | D. | ?x0≥0,x${\;}_{0}^{2}$≥2${\;}^{{x}_{0}}$ |
分析 根据含有量词的命题的否定为:将任意改为存在,结论否定,即可写出命题的否定
解答 解:命题p:?x<0,x2≥2x,则命题¬p为?x0<0,x${\;}_{0}^{2}$<2${\;}^{{x}_{0}}$,
故选:C
点评 本题的考点是命题的否定,主要考查含量词的命题的否定形式:将任意与存在互换,结论否定即可.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案
相关题目
20.在${({\sqrt{x}+\frac{3}{x}})^n}$的展开式中,各二项式系数之和为64,则展开式中常数项为( )
| A. | 135 | B. | 105 | C. | 30 | D. | 15 |
1.已知抛物线C:y2=8x的焦点为F,准线为l,P是l上一点,Q是直线PF与C的一个交点,若$\overrightarrow{FQ}=-4\overrightarrow{FP}$,则|QF|=( )
| A. | 35 | B. | $\frac{5}{2}$ | C. | 20 | D. | 3 |
18.设复数z满足$\overline{z}$=|1-i|+i(i为虚数单位),则复数z为( )
| A. | $\sqrt{2}$-i | B. | $\sqrt{2}$+i | C. | 1 | D. | -1-2i |
15.曲线x2+(y-1)2=1(x≤0)上的点到直线x-y-1=0的距离最大值为a,最小值为b,则a-b的值是( )
| A. | $\sqrt{2}$ | B. | 2 | C. | $\frac{\sqrt{2}}{2}$+1 | D. | $\sqrt{2}$-1 |
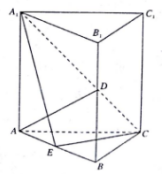 如图,正三棱柱ABC-A1B1C1的所有棱长均为2,D,E分别是BB1和AB的中点.
如图,正三棱柱ABC-A1B1C1的所有棱长均为2,D,E分别是BB1和AB的中点.