题目内容
2.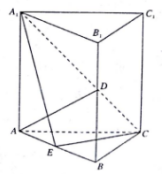 如图,正三棱柱ABC-A1B1C1的所有棱长均为2,D,E分别是BB1和AB的中点.
如图,正三棱柱ABC-A1B1C1的所有棱长均为2,D,E分别是BB1和AB的中点.(1)证明:AD⊥平面A1EC;
(2)求点B1到平面A1EC的距离.
分析 (1)以E为原点,EB为x轴,EC为y轴,过E作平面ABC的垂线为z轴,建立空间直角坐标系,利用向量法能证明AD⊥平面A1EC.
(2)求出$\overrightarrow{E{B}_{1}}$=(1,0,2),平面A1EC的法向量$\overrightarrow{AD}$=(2,0,1),利用向量法能求出点B1到平面A1EC的距离.
解答 证明:(1)以E为原点,EB为x轴,EC为y轴,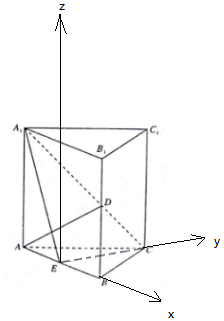
过E作平面ABC的垂线为z轴,建立空间直角坐标系,
则A(-1,0,0),D(1,0,1),A1(-1,0,2),
E(0,0,0),C(0,$\sqrt{3}$,0),
$\overrightarrow{AD}$=(2,0,1),$\overrightarrow{E{A}_{1}}$=(-1,0,2),$\overrightarrow{EC}$=(0,$\sqrt{3}$,0),
∵$\overrightarrow{AD}•\overrightarrow{E{A}_{1}}=-2+2=0$,$\overrightarrow{AD}•\overrightarrow{EC}$=0,
∴AD⊥EA1,AD⊥EC,
∵EA1∩EC=E,∴AD⊥平面A1EC.
解:(2)B1(1,0,2),$\overrightarrow{E{B}_{1}}$=(1,0,2),
∵AD⊥平面A1EC,
∴平面A1EC的法向量$\overrightarrow{AD}$=(2,0,1),
∴点B1到平面A1EC的距离d=$\frac{|\overrightarrow{E{B}_{1}}•\overrightarrow{AD}|}{|\overrightarrow{AD}|}$=$\frac{4}{\sqrt{5}}=\frac{4\sqrt{5}}{5}$.
点评 本题考查线面垂直的证明,考查点到平面的距离的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

| A. | ?x0<0,x${\;}_{0}^{2}$≥2${\;}^{{x}_{0}}$ | B. | ?x0≥0,x${\;}_{0}^{2}$≥2${\;}^{{x}_{0}}$ | ||
| C. | ?x0<0,x${\;}_{0}^{2}$<2${\;}^{{x}_{0}}$ | D. | ?x0≥0,x${\;}_{0}^{2}$≥2${\;}^{{x}_{0}}$ |
| A. | e2f(2)>e3f(3) | B. | e2f(2)<e3f(3) | C. | e2f(2)≥e3f(3) | D. | e2f(2)≤e3f(3) |
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -1 | D. | 2 |
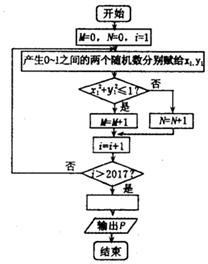 如图所示,使用模拟方法估计圆周率值的程序框闰,P表示估计的结果,刚图中空白框内应填入P=( )
如图所示,使用模拟方法估计圆周率值的程序框闰,P表示估计的结果,刚图中空白框内应填入P=( )| A. | $\frac{M}{2017}$ | B. | $\frac{2017}{M}$ | C. | $\frac{4M}{2017}$ | D. | $\frac{2017}{4M}$ |
 如图,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$与双曲线$\frac{x^2}{4}-\frac{y^2}{2}=1$有相同的焦点,且椭圆C过点P(2,1),若直线l与直线OP平行且与椭圆C相交于点A,B.
如图,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$与双曲线$\frac{x^2}{4}-\frac{y^2}{2}=1$有相同的焦点,且椭圆C过点P(2,1),若直线l与直线OP平行且与椭圆C相交于点A,B.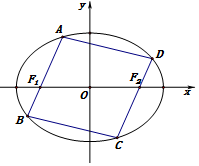 已知椭圆E的中心在原点,焦点F1、F2在x轴上,离心率为$\frac{1}{2}$,在椭圆E上有一动点A与F1、F2的距离之和为4,
已知椭圆E的中心在原点,焦点F1、F2在x轴上,离心率为$\frac{1}{2}$,在椭圆E上有一动点A与F1、F2的距离之和为4,