题目内容
5.已知f(x)=$\sqrt{3}$sin(π+ωx)•sin($\frac{3}{2}$π-ωx)-cos2ωx(ω>0)的最小正周期为T=π.(1)求f($\frac{4π}{3}$)的值.
(2)在△ABC中,角A,B,C所对的边分别为a,b,c,若(2a-c)cosB=bcosC,求角B的大小以及f(A)的取值范围.
分析 (1)f(x)=$\sqrt{3}$sin(π+ωx)•sin($\frac{3}{2}$π-ωx)-cos2ωx=)=$\sqrt{3}$sinωx•cosωx-cos2ωx
=$\frac{\sqrt{3}}{2}sin2ωx-\frac{1}{2}cos2ωx-\frac{1}{2}$=sin(2ωx-$\frac{π}{6}$)-$\frac{1}{2}$.由最小正周期得ω
(2)由(2a-c)cosB=bcosC得(2sinA-sinC)cosB=sinBcosC,
cosB、B,再求f(A)的取值范围
解答 解:(1)f(x)=$\sqrt{3}$sin(π+ωx)•sin($\frac{3}{2}$π-ωx)-cos2ωx=$\sqrt{3}$sinωx•cosωx-cos2ωx
=$\frac{\sqrt{3}}{2}sin2ωx-\frac{1}{2}cos2ωx-\frac{1}{2}$=sin(2ωx-$\frac{π}{6}$)-$\frac{1}{2}$.
∵最小正周期为T=π,∴$\frac{2π}{2ω}=π$,⇒ω=1.
∴f(x)=sin(2x-$\frac{π}{6}$)-$\frac{1}{2}$
∴f($\frac{4π}{3}$)=sin(2×$\frac{4π}{3}-\frac{π}{6}$)-$\frac{1}{2}$=$\frac{1}{2}$.
(2)∵(2a-c)cosB=bcosC,∴(2sinA-sinC)cosB=sinBcosC,
2sinAcosB=sinBcosC+cosBsinC=sin(B+C)=sinA.
∵sinA>0,∴cosB=$\frac{1}{2}$,∵B∈(0,π),∴$B=\frac{π}{3}$.
∴A$∈(0,\frac{2π}{3})$,2A-$\frac{π}{6}$$∈(-\frac{π}{6},\frac{7π}{6})$,∴sin(2A-$\frac{π}{6}$)$∈(-\frac{1}{2},1]$.
f(A)的取值范围:(-1,$\frac{1}{2}$].
点评 本题考查了三角恒等变形,解三角形,属于中档题.

 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案| A. | y=lnx3 | B. | y=-x2 | C. | y=-$\frac{1}{x}$ | D. | y=x|x| |
| A. | (1)(3) | B. | (2)(4) | C. | (2)(3)(4) | D. | (1)(2)(3)(4) |
| A. | ?x0<0,x${\;}_{0}^{2}$≥2${\;}^{{x}_{0}}$ | B. | ?x0≥0,x${\;}_{0}^{2}$≥2${\;}^{{x}_{0}}$ | ||
| C. | ?x0<0,x${\;}_{0}^{2}$<2${\;}^{{x}_{0}}$ | D. | ?x0≥0,x${\;}_{0}^{2}$≥2${\;}^{{x}_{0}}$ |
| A. | e2f(2)>e3f(3) | B. | e2f(2)<e3f(3) | C. | e2f(2)≥e3f(3) | D. | e2f(2)≤e3f(3) |
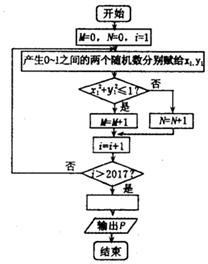 如图所示,使用模拟方法估计圆周率值的程序框闰,P表示估计的结果,刚图中空白框内应填入P=( )
如图所示,使用模拟方法估计圆周率值的程序框闰,P表示估计的结果,刚图中空白框内应填入P=( )| A. | $\frac{M}{2017}$ | B. | $\frac{2017}{M}$ | C. | $\frac{4M}{2017}$ | D. | $\frac{2017}{4M}$ |
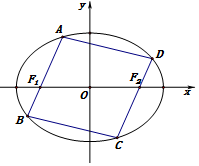 已知椭圆E的中心在原点,焦点F1、F2在x轴上,离心率为$\frac{1}{2}$,在椭圆E上有一动点A与F1、F2的距离之和为4,
已知椭圆E的中心在原点,焦点F1、F2在x轴上,离心率为$\frac{1}{2}$,在椭圆E上有一动点A与F1、F2的距离之和为4,